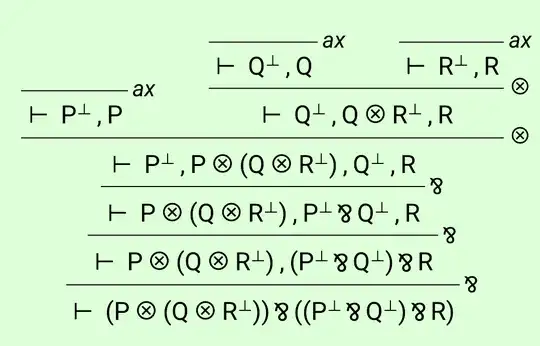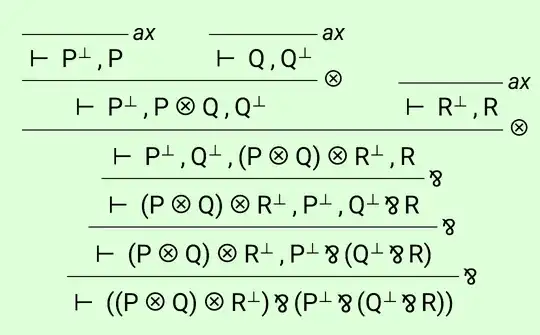2

I’ve been trying to use https://click-and-collect.linear-logic.org for a while, and have been thinking about exportation/importation for Linear Logic. Intuitively, I thought P⊸(Q⊸R)≡(P⊗Q)⊸R was valid in Linear Logic, and this is supported by Noam Zeilberger’s answer to this question:Is currying valid in Linear logic and Relevance logic?. I tried to see if the prover I mentioned would give a sequent calculus proof, and it comes back as invalid each time I use it. The thing is that linear implication is not used by the prover, so any formula using linear implication is translated by the prover into a formula containing only tensor, par, and negation. The only way I could see how this would be invalid then is if the usual “implies left” rule is not valid for linear implication. Is this the case, or is the prover incorrect

Edit: It turns out I didn’t read the instructions carefully enough and wasn’t using the prover correctly.

PW_246
  • 1,604
  • 2
    I was able to prove the equivalence using the tool. In my experience, the non-obvious step was the rearranging of the formulas (exchange structural rule) which is needed before clicking on the tensors so to choose how to split the context of the tensor between the two premises (otherwise we get stuck) . Rearranging is done using drag & drop. Maybe you missed that feature? – chi Aug 30 '23 at 13:58
  • Yeah I didn’t really read the instructions so I was doing it wrong. – PW_246 Aug 30 '23 at 17:51

2 Answers2

6

I tried to see if the prover I mentioned would give a sequent calculus proof, and it comes back as invalid each time I use it [..] The only way I could see how this would be invalid then is if the usual “implies left” rule is not valid for linear implication. Is this the case, or is the prover incorrect?

Neither. The equivalence P⊸(Q⊸R)≡(P⊗Q)⊸R is valid, the implication left rule is correct, and the tool behaves correctly as well, producing the two expected proofs (one for each direction).

If it comes back invalid each time you invoke it, the most likely explanation is that you somehow use it wrong, and that's why you get unexpected results.

Alas, I can't diagnose what went wrong for you, since you did not describe what you did with the prover in any detail.

You can produce the proofs yourself by copy-pasting your formula into the textbox, replacing the equivalence symbol with a $\vdash$, clicking prove, then double-clicking the turnstile to auto-complete the proof.

For the sake of completeness, proofs generated by the tool are shown on the screenshots below:

A linear logic proof that P⊸(Q⊸R) implies (P⊗Q)⊸R, produced by the linked tool A linear logic proof that (P⊗Q)⊸R implies P⊸(Q⊸R)

Z. A. K.
  • 13,310
2

Encoding into negation, par and tensor, I believe the following sequence of equivalences is valid:

$$P ⊸ (Q ⊸ R) =\\ P^⊥ ⅋ (Q^⊥ ⅋ R) = \\ (P^⊥ ⅋ Q^⊥) ⅋ R = \\ (P \otimes Q)^⊥ ⅋ R = \\ P \otimes Q ⊸ R$$

So presumably the solver is incomplete or is purposely not considering one (or more) of those equivalences.

Dan Doel
  • 4,608