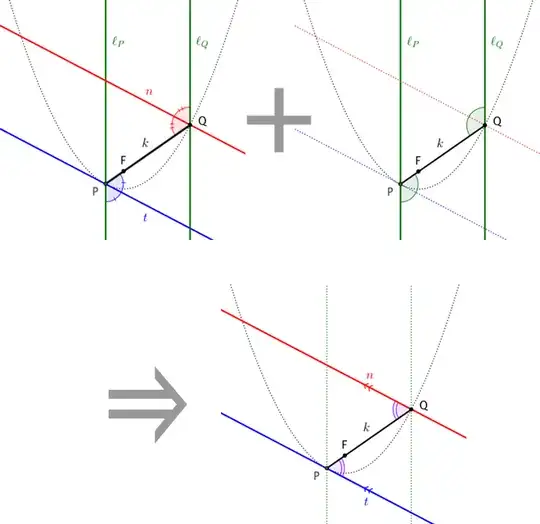
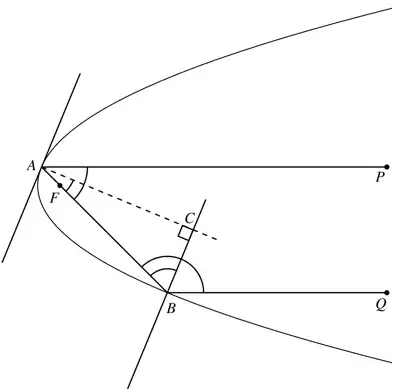
Prove that in a parabola the tangent at one end of a focal chord is parallel to the normal at the other end.

Question

Prove that in a parabola the tangent at one end of a focal chord is parallel to the normal at the other end.

Now, I know prove this algebraically, and that's very easy, but I am not getting any visual picture of the above situation. It'd be great if someone could give a proof without (or with minimal) words for this one - these proofs are exciting!

EDIT: A quick-n-dirty working of what I call an algebraic proof:

WLOG, let the equation of the parabola be $y^2 = 4ax$. The coordinates of points on the focal chord and also on the parabola are: $ P(at^2,2at) $ and $Q(al^2, 2am)$. For these points to lie on a focal chord, $ tm = -1 $. The tangent at $P$ is given as $ y(2at) = 2a(x+at^2) $ so the slope is $1/t$. Similarly the slope of tangent at $Q$ is $1/m$. So the slope of the normal at $Q$ is $-m = 1/t = $ slope of tangent at $P$.

Now, I know I am using some 'shortcuts' here, but then this was just a fast-paced look at what I did. The point is, I know how to prove the statement using the regular 'equations approach'. I want to know if there are any visual proofs.

Answer 1

Let $k := \overleftrightarrow{PQ}$ be a line containing focal chord $\overline{PQ}$. Let lines $\ell_P$ and $\ell_Q$, through $P$ and $Q$, respectively, be parallel to the parabola's axis.

By the Reflection Property of Parabolas, the normal and tangent at $P$ bisect angles made by $k$ and $\ell_P$; likewise, at $Q$. In particular, the tangent at $P$ (call it $t$) and the normal at $Q$ (call it $n$) bisect alternate interior angles formed by parallel lines $\ell_P$ and $\ell_Q$ cut by transversal $k$. These angles are congruent, so their half-angles are congruent. A pair of such half-angles comprise the alternate interior angles of $t$ and $n$ cut by $k$, whence $t \parallel n$: the tangent at $P$ is parallel to the normal at $Q$.

---

Proof without words

Answer 2

In the following diagram, the axis of the parabola is horizontal and the focus $F$ is at the dot. The line through the focus intersects the parabola at $A$ and $B$.

$\hspace{3.2cm}$

Note that $\angle PAB$ and $\angle ABQ$ are supplementary (they sum to $\pi$) since $\overline{AP}$ and $\overline{BQ}$ are both parallel to the axis. By the reflection property for parabolas, $\overline{AC}$, being perpendicular to the tangent at $A$, bisects $\angle PAB$, and $\overline{BC}$, being normal to the parabola at $B$, bisects $\angle ABQ$. Thus, $\angle CAB$ and $\angle CBA$ are complementary (they sum to $\pi/2$), and therefore, $\triangle ACB$ is a right triangle. Since $\overline{AC}$ is perpendicular to the tangent at $A$ and perpendicular to the normal at $B$, the tangent at $A$ and the normal at $B$ are parallel.

Answer 3

Here's a geometric proof, based on the fact that a line (thought of as a light ray) going through the focus of a parabola reflects to a line parallel to the axis of the parabola. This is sometimes called the reflective property of the parabola. Call the focus $F$, and have the parabola arranged with its axis the $y$ axis. Pick the chord $BA$ through $F$, so that $A$ lies to the right of $F$ and $B$ to the left.

We need to name some reference points: Pick a point $A_L$ to the left of $A$ on the tangent line $T_A$, and another point $A_R$ to its right. Similarly pick the points $B_L,B_R$ to the left and right of $B$ on the tangent line $T_B$. Also pick a point $A'$ above $A$ on the vertical through $A$ and another point $A''$ below $A$ on that vertical; similarly pick points $B'$ and $B''$ above and below $B$ on the vertical through $B$.

Now the reflective property of the parabola means in this notation that the angles $A_LAF$ and $A'AA_R$ are equal. Call that common angle $\alpha$, and note that by the vertical angle theorem (opposite angles of intersecting lines are equal) we also have $\alpha$ equal to the angle $A_LAA''.$

Similarly we have the three equal angles, call each $\beta$, namely angles $B_RBF$ and $B_LBB'$ from the reflective property and the further equal angle in this triple $B_RBB''$ again from the vertical angle theorem.

Now because the segment $BA$ may be extended to a line transverse to the two parallel verticals through $A$ and $B$, we have that angle $B''BB_R$ is equal to angle $BAA'$. A diagram shows that the first of these is $2\beta$, while the second is $\pi-2\alpha$. This brings us almost to the end of the argument, since we now have $\alpha+\beta=\pi.$ So if we let the two tangent lines $T_A,\ T_B$ meet at the point $P$, we see (again referring to a sketch) that triangle $BPA$ is a right triangle with its right angle at $P$. But this means the two tangent lines $T_A,\ T_B$ are perpendicular, so we may conclude finally that the normal line $N_B$ through $B$ is parallel to the tangent line $T_A$ at $A$.