0

I summarize what I saw in part of this post as assertion:

\begin{aligned} |ab| > 1+\frac{3}{2}\pi, |a|<1 \Rightarrow \sum\limits_{0}^{\infty}(ab)^n \pi\sin(b^n\pi x) \ \text{diverges} \end{aligned}

Although I think we have to add $x \neq 0$ condition.

Referenced post remind $\sum\limits_{0}^{\infty}|r|^n$ and compares above series with it:

The trigonometric functions complicate it somewhat, making us need $|ab|$ to be greater than $1+\frac{3}{2}\pi$, but the basic idea survives.

So I tried somethings for proving that assertioin:

  • I did the ratio test but could not calculate this limit: $$\lim\limits_{n \to \infty} ab\frac{\sin(b^{n+1}\pi x)}{\sin(b^{n}\pi x)}$$
  • Also no success in showing $\lim\limits_{n \to \infty} (ab)^{n}{\sin(b^{n}\pi x)} \neq 0$ to use nth-term test.
  • and so on no success on other tries for proving.
  • I tried a sample with GNU Octave too to get an idea:
a=2/3;    
b=9;     
x=linspace (0,2/b,1000);    
data = [];    
for n =1:100    
   y=(a*b)^(n+1) *sin(b^(n+1)*pi*x) - (a*b)^(n)*sin(b^(n)*pi*x);    
   data = [data; n min(y) max(y)];    
endfor

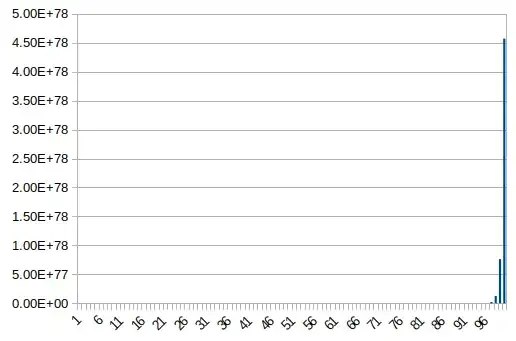
Below charts show min(y) and max(y) for different values of n:

enter image description here enter image description here

Although above charts show that growth speed is very rapid (like exponential functions); but again I could not find a way to prove it.

Now

  • I want to know is there a simple prove for above assertion?
  • Also I want to know are $|ab| > 1+\frac{3}{2}\pi, |a|<1$ conditions necessary for series to be divergence? Or those are sufficient?
hasanghaforian
  • 761
  • 1
    No, the condition is not necessary. $|ab|=1$ still gives a function that is not differentiable at all irrational points and some rational points. The sufficient condition was introduced by Weierstraß for an easier proof, for a suitable interpretation of "easy". See https://math.stackexchange.com/questions/869551/are-there-standard-parameters-for-the-weierstrass-nowhere-differentiable-functio for more extensive remarks (but still no proof idea). – Lutz Lehmann Aug 15 '23 at 15:47

1 Answers1

1

A necessary condition for a series $\sum_nc_n$ to converge is that $c_n\to 0$.

Assume that the series converges. If $|ab|\ge 1$, then $(ab)^n$ does not go to zero, which means that $\sin(b^n\pi x)$ must go to zero. But this implies that $x=\frac{p}{b^q}$ where $p$ and $q$ are integers so that $\sin(b^n\pi x)=0$ for $n>q$. This is a lemma in a paper of Hardy Lemma 2,15

For all $x$ not of that type, $\sin(b^n\pi x)$ does not go to zero, and since $|(ab)^n\sin(b^n\pi x)|\ge|\sin(b^n\pi x)|$, the series cannot converge.

Gio67
  • 21,870