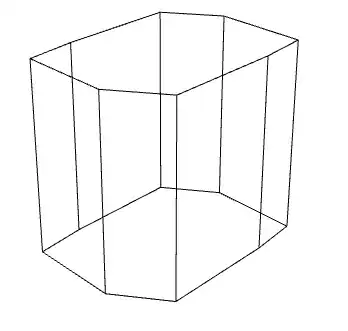
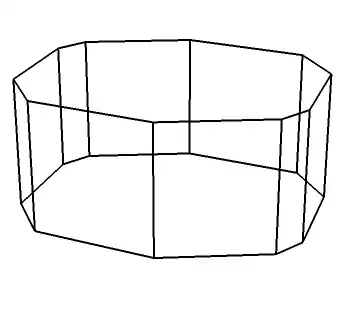
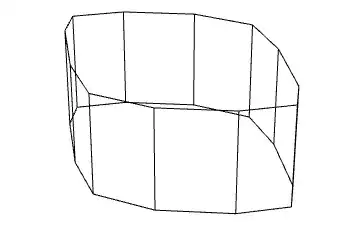
A zonogon is a convex polygon that is made up of pairs of parallel line segments that are congruent. A zonogonal cylinder is a cylinder with identical and identically aligned zonogons as the end caps. A cuboid is a special case of a zonogonal cylinder. Thus, this is a generalization of the question: Orthogonal Projection Area of a 3D Cuboid.
Here are four examples of a zonogonal cylinder:
Both zonogons and zonogonal cylinders are centrally symmetric around an axis. And the orthographic projection of a zonogonal cylinder is also always a zonogon. The minimum amount of sides of a $2n$-zonogonal cylinder's orthographic projection is always 4 because from one side it can be a rectangle. And I believe the maximum number of sides of the orthographic projection is exactly $2n+2$.
The format of the solution likely follows the same format for the cuboid, like: $$\sum{(\text{face area}\cdot\prod{\text{trig functions}})}$$
I am giving the code to calculate it numerically in Mathematica as well as in JavaScript so that way it is easier to understand and accessible.
MATHEMATICA CODE:
First, have to create a random zonogon. This is from the SHuisman's code:
ClearAll[CreateRandomZonogon]
CreateRandomZonogon[sides_?EvenQ, lendist : {min_, max_}] :=
Module[{m, angles, dirs, lengths},
m = sides/2;
angles = RandomReal[{0, 1}, m];
angles /= Total[angles]/(Pi);
angles = Join[angles, angles];
dirs = Accumulate[angles];
dirs += RandomReal[{0, 2 Pi}];
lengths = RandomReal[lendist, m];
lengths = Join[lengths, lengths];
Polygon[Accumulate[MapThread[AngleVector[{#1, #2}] &, {lengths, dirs}]]]
]
Now, we can numerically find the area:
endcapPolygonShape = CreateRandomZonogon[6, {0.5, 10}];
endcapPolygonShapeCoordinates = PolygonCoordinates[endcapPolygonShape];
zonogonalCylinderHeight = RandomInteger[{1, 10}];
bottomZonogalEndcap = Map[Append[#, 0]&,endcapPolygonShapeCoordinates];
topZonogalEndcap = Map[Append[#, zonogonalCylinderHeight]&,endcapPolygonShapeCoordinates];
zonogonalCylinderPoints = Join[bottomZonogalEndcap,topZonogalEndcap];
α = RandomReal[{0,2π}];
β = RandomReal[{0,2π}];
γ = RandomReal[{0,2π}];
rotationMatrixTransorm = Transpose[RollPitchYawMatrix[{β, α, γ},{3,2,1}]];
rotatedBoxPoints = Dot[zonogonalCylinderPoints,rotationMatrixTransorm];
xyProjectionPoints = Drop[rotatedBoxPoints,0,-1];
silouetteArea = Area[ConvexHullRegion[xyProjectionPoints]]
JAVASCRIPT CODE:
NOTE: The made first function to create the random zonogon by taking Vitaliy Kaurov's 'stretching' approach in Mathematica and converted it.
function createZonogon(n) {
let pointsArr = [];
let rotateAngle = Math.random() * 360;
let scaleX = 0.5 + Math.random();
let scaleY = 0.5 + Math.random();
let skewX = Math.random() * 60 - 30;
let skewY = Math.random() * 60 - 30;
let radianRotate = (Math.PI / 180) * rotateAngle;
let sinRotate = Math.sin(radianRotate);
let cosRotate = Math.cos(radianRotate);
let radianSkewX = (Math.PI / 180) * skewX;
let radianSkewY = (Math.PI / 180) * skewY;
for (let i = 0; i < n; i++) {
let angle = 2 * Math.PI * i / n;
let x = 250 + 100 * Math.cos(angle);
let y = 250 + 100 * Math.sin(angle);
// Apply transformations directly:
// Rotation
let rotatedX = cosRotate * x - sinRotate * y;
let rotatedY = sinRotate * x + cosRotate * y;
// Scaling
let scaledX = rotatedX * scaleX;
let scaledY = rotatedY * scaleY;
// Skewing
let skewedX = scaledX + scaledY * Math.tan(radianSkewX);
let skewedY = scaledY + scaledX * Math.tan(radianSkewY);
pointsArr.push([skewedX, skewedY]);
}
return pointsArr;
}
function rotate3DPoints(points, alpha, beta, gamma) {
// Define the rotation matrix based on alpha, beta, and gamma
let matrix = [
[
Math.cos(alpha) * Math.cos(beta),
Math.cos(gamma) * Math.sin(beta) + Math.cos(beta) * Math.sin(alpha) * Math.sin(gamma),
-Math.cos(beta) * Math.cos(gamma) * Math.sin(alpha) + Math.sin(beta) * Math.sin(gamma)
],
[
-Math.cos(alpha) * Math.sin(beta),
Math.cos(beta) * Math.cos(gamma) - Math.sin(alpha) * Math.sin(beta) * Math.sin(gamma),
Math.cos(gamma) * Math.sin(alpha) * Math.sin(beta) + Math.cos(beta) * Math.sin(gamma)
],
[
Math.sin(alpha),
-Math.cos(alpha) * Math.sin(gamma),
Math.cos(alpha) * Math.cos(gamma)
]
];
// Apply the rotation matrix to the points
return points.map(point => {
let x = point[0];
let y = point[1];
let z = point[2];
let rotatedX = matrix[0][0] * x + matrix[0][1] * y + matrix[0][2] * z;
let rotatedY = matrix[1][0] * x + matrix[1][1] * y + matrix[1][2] * z;
let rotatedZ = matrix[2][0] * x + matrix[2][1] * y + matrix[2][2] * z;
return [rotatedX, rotatedY, rotatedZ];
});
}
function computeCentroid(points) {
let xSum = 0, ySum = 0;
for (let p of points) {
xSum += p[0];
ySum += p[1];
}
return [xSum / points.length, ySum / points.length];
}
function sortPointsByAngle(points, centroid) {
points.sort((a, b) => {
return Math.atan2(a[1] - centroid[1], a[0] - centroid[0]) - Math.atan2(b[1] - centroid[1], b[0] - centroid[0]);
});
}
function projectTo2D(points) {
return points.map(p => [p[0], p[1]]);
}
function shoelace(points) {
let n = points.length;
let area = 0;
for (let i = 0; i < n - 1; i++) {
area += points[i][0] * points[i+1][1] - points[i+1][0] * points[i][1];
}
area += points[n-1][0] * points[0][1] - points[0][0] * points[n-1][1];
return 0.5 * Math.abs(area);
}
function computeSilhouetteArea() {
let zonogon = createZonogon(6);
let height = Math.floor(Math.random() * 10) + 1;
// Convert to 3D and extrude
let allPoints = zonogon.map(p => [p[0], p[1], 0]).concat(zonogon.map(p => [p[0], p[1], height]));
// Random rotations
let alpha = Math.random() * 2 * Math.PI;
let beta = Math.random() * 2 * Math.PI;
let gamma = Math.random() * 2 * Math.PI;
let rotatedPoints = rotate3DPoints(allPoints, alpha, beta, gamma);
let projectedPoints = projectTo2D(rotatedPoints);
let centroid = computeCentroid(projectedPoints);
sortPointsByAngle(projectedPoints, centroid);
return shoelace(projectedPoints);
}
console.log(computeSilhouetteArea());