I want to learn how to use the Karush-Kuhn-Tucker (KKT) conditions to solve a quadratic programming problem with both equality and in-equality constraints.
The problem in question is set in finance and it consists in finding the best constantly re-balanced portfolio in hindsight, i.e. a portfolio that maximizes the logarithmic wealth in hindsight. In other words, given a matrix of multivariate returns $ \left( R_{i,t} \right)_{i,t=1,1}^{N,T} $we are looking for a vector $ {\bf b} := \left( b_i \right)_{i=1}^N $ such that :
\begin{equation} {\bf b}^{*} = \mbox{argmax}_{{\bf b}} \sum\limits_{\xi=1}^T \log(1 + {\bf b} \cdot \vec{R}_\xi ) \tag{1} \end{equation}
subject to the following constraints:
- No leverage: $ |{\bf b}| = b_1+b_2+ \cdots + b_N = 1$,
- No short selling: $ b_i \ge 0 $ for $i=1,\cdots, N$.
Note 1:
In practice, problem $(1)$ can be formulated as a quadratic minimization problem. In fact by expanding the logarithm in a series to the second order we need to solve the following:
\begin{equation} {\bf b}^{*} = \mbox{argmin}_{{\bf b}} \sum\limits_{\xi=1}^T \left( - {\bf b} \cdot \vec{\mu} + \frac{1}{2} {\bf b}^{T} \cdot {\bf c} \cdot {\bf b} \tag{2} \right) \end{equation}
where $ \vec{\mu} = \left( \mu_i\right)_{i=1}^N $ where $\mu_i = \sum\limits_{\xi=1}^T R_{i,\xi} $ for $i=1,\cdots,N$ and ${\bf c}:= \left( c_{i,j} \right)_{i,j=1}^N$ where $ c_{i,j} := \sum\limits_{\xi=1}^T R_{i,\xi} R_{j,\xi} $ for $i,j,=1,\cdots,N $.
Note 2:
The solution to the unconstrained problem, i.e. with the constraints 2. being waived, reads:
\begin{equation} {\bar {\bf b}}^{*} = {\bf c}^{-1} \cdot \left( \vec{\mu} - \lambda 1_{N \times 1}\right) \tag{3} \end{equation}
where $1_{N \times 1}$ is a column vector of length $N$ composed of ones and the constant $\lambda $ satisfies the following equation $1_{N,1}^{T} \cdot {\bf c}^{-1} \left( \vec{\mu} - \lambda \right) = 1 $.
Now, I have followed the Numerical Example in here to code the KKT conditions. In short what I do is the following. I start with the solution $(3)$ and then find which in-equality constraints (no short-selling) are violated. Then I make those constraints active, i.e. I add those constraints to the the Lagrange function. In other words my new Lagrange function reads:
\begin{equation} L\left( {\bf b}; {\bf \kappa}, \lambda \right) := - {\bf b} \cdot \vec{\mu} + \frac{1}{2} {\bf b}^{T} \cdot {\bf c} \cdot {\bf b} + \sum\limits_{j=1, j\in {\mathfrak J}}^{N} \kappa_j \cdot (-b_j) + \lambda \left( \left| {\bf b} \right| - 1 \right) \tag{4} \end{equation}
where ${\mathfrak J} := \left( j \in \left\{1,\cdots, N \right\} | b^{*}_j < 0 \right) = \left( \eta_1,\eta_2, \cdots, \eta_m\right) $ and $ {\bar {\bf b}}^{*} := \left( b^{*}_j\right)_{j=1}^N $.
Now, by taking the gradient of $(4)$ by the allocation vector and setting it to zero we get:
\begin{eqnarray} \frac{\partial }{\partial b_i} L\left( {\bf b}; {\bf \kappa}, \lambda \right) = - \mu_i + \sum\limits_{j=1}^N {\bf c}_{i,j} {\bf b}_j + \sum\limits_{j=1, j\in {\mathfrak J}}^{N} \kappa_j \cdot (-\delta_{j,i}) + \lambda &=& 0 & \quad \mbox{for $i=1,\cdots,N$} \tag{5a} \\ b_j &=& 0 & \quad \mbox{for $j \in {\mathfrak J}$} \tag{5b} \\ b_1+b_2 + \cdots b_{N} &=& 1 \tag{5c} \end{eqnarray} where $m := card({\mathfrak J}) $.
The equations $(5a)-(5c)$ constitute a system of $N + m$ linear equations with unknowns $\vec{r}:= \left(b_1,b_2,\cdots,b_N;\kappa_{\eta_1},\cdots,\kappa_{\eta_m}; \lambda\right)$. I solve the aforementioned equations by solving a following system of linear equations:
\begin{equation} \left( \begin{array}{lll} {\bf c} & - {\bf m}_{1,2} & {\bf 1}_{N,1} \\ -{\bf m}_{1,2}^{T} & {\bf 0}_{m,m} & {\bf 0}_{m,1} \\ {\bf 1}_{1,N} & {\bf 0}_{1,m} & {\bf 0}_{1,1} \end{array} \right) \cdot \vec{r} = \left( \begin{array}{l} \vec{\mu} \\ {\bf 0}_{m,1} \\ 1 \end{array} \right) \tag{6} \end{equation}
where $ {\bf m}_{1,2} := \left( \delta_{\eta_j, i} \right)_{i=1,j=1}^{N,m} $
I have written a simple program in Matlab that codes equations $(6)$ as below.
%This is to test the quadratic programming algo with both equality and
%in-equality constraints as formulated in the Example in
%https://optimization.cbe.cornell.edu/index.php?title=Quadratic_programming.
close all;
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
% Generate the time series.
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
tmp = rand(1,6); [r1,r2,r3,z12,z13,z23]=deal(tmp(1),tmp(2),tmp(3),tmp(4),tmp(5),tmp(6));
%Number of assets and the length of time series.
dim = randi([10,20],1);p1 = randi([1,dim-2],1);p2 = randi([p1+1,dim-1],1);T = 1000;dt= 1/256;
% The underlying correlation matrix and the drifts,
Sigma = ConstructBlockDiagonalMatrix([r1 z12 z13; z12 r2 z23; z13 z23 r3],[p1, p2-p1 dim-p2]);
mu = rand(dim,1)/256;
R= randn(dim,T);
% The prices S, the returns R and the price relatives X.
S = cumprod(1 + mu*dt + Sigma*sqrt(dt)*R,2);
R = diff(S,1,2)./S(:,1:end-1);
X = S(:,2:end)./S(:,1:end-1);
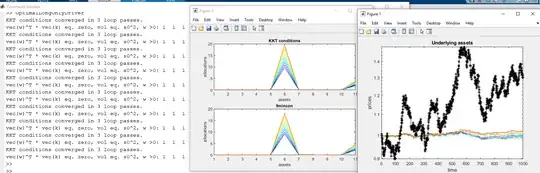
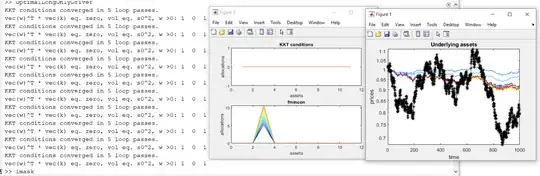
figure; semilogy(S');xlabel('time');ylabel('prices');
%An approximate closed form expression for bstar.
%Old way.
[rhs,mat] = deal(zeros(dim-1,1),zeros(dim-1));
for xi=1:dim-1
rhs(xi) = sum((R(xi,:) - R(xi+1,:)) ./ (1+R(dim,:)));
for eta=1:dim-1
mat(xi,eta) = sum((R(xi,:) - R(xi+1,:)) .* (R(eta,:) - R(eta+1,:)) ./ (1+R(dim,:)).^2);
end
end
bstarApr = mat \ rhs;
bstarApr =[bstarApr(1) diff(bstarApr)' 1-bstarApr(end)]';
%New way.
[rhs,mat] = deal(zeros(dim,1),zeros(dim));
for xi=1:dim
rhs(xi) = sum(R(xi,:));
for eta=1:dim
mat(xi,eta) = sum( R(xi,:) .* R(eta,:) );
end
end
mones = ones(1,dim);
lmb= ( mones (mat \ rhs) - 1 )/( mones (mat \ mones') );
bstarApr1 = mat \ (rhs - lmb * ones(dim,1));
bstarApr2=quadprog(mat,-rhs,[],[],ones(1,dim),1);
%Solve the constrained problem by using the Karush-Kuhn-Tucker theorem https://en.wikipedia.org/wiki/Karush-Kuhn-Tucker_conditions
%See also example from https://optimization.cbe.cornell.edu/index.php?title=Quadratic_programming
Theta1 = find(bstarApr1 < 0);
dim1 = length(Theta1);
mat12 = -cell2mat(arrayfun(@(xi) (xi == Theta1), 1:dim, 'UniformOutput', false))';
Mat = ...
{ mat, mat12, ones(dim,1); ...
-mat12', zeros(dim1,dim1), zeros(dim1,1); ...
ones(1,dim), zeros(1,dim1), zeros(1,1)};
Mat=cell2mat(Mat);
% Sanity check:
% 2x1 & 3x1 block:
all(arrayfun(@(xi) Mat(dim+xi,Theta1(xi)),1:dim1 )==1)
all(Mat(dim+dim1+1,1:dim)==1)
% 1x2 block:
all(arrayfun(@(p) Mat(Theta1(p),dim+p),1:dim1)==-1)
Rhs={rhs; zeros(dim1,1); ones(1)};
Rhs= cell2mat(Rhs);%Rhs(end)=[];
Vars = Mat \ Rhs;
[Mu1] = deal(Vars(dim+(1:dim1)));
%Drop constraints for which Mu's are negative.
Theta1new = Theta1; Theta1new(Mu1 <0 )=[];
bstarConstr=quadprog(mat,-rhs,-eye(dim),zeros(1,dim),ones(1,dim),1);
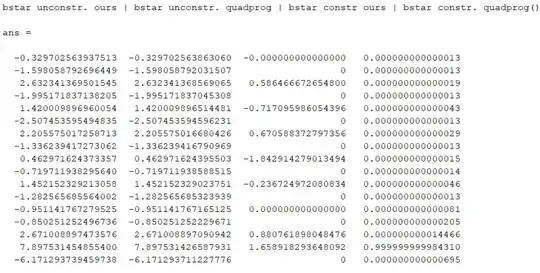
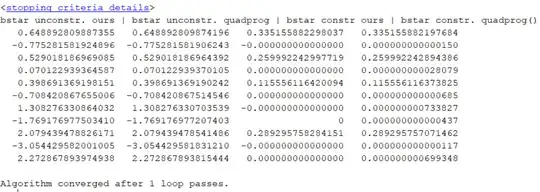
disp('bstar unconstr. ours | bstar unconstr. quadprog | bstar constr ours | bstar constr. quadprog()');
[bstarApr1, bstarApr2, Vars(1:dim) bstarConstr]
This program outputs the un-constrained solution $(3)$ along with the output of Matlab's quadprog() routine (the first two columns on the left) and the constrained solution along with the respective quadprog output (last two columns on the right).
As you can see the first two columns match (as they should) but the last two columns don't.
In view of that I have two following questions.
The first question is what it is that I am doing wrong in the calculations above?
The second question is how would you be using the KKT conditions to solve the Markowitz portfolio optimization problem, i.e. to maximize the mean return of the portfolio subject to a given variance (volatility) and subject to all the asset allocations being non-negative (long only).