Solving $\partial_t \gamma_t(x) = - \gamma_t(x) + \frac{\gamma_t''(x)}{\gamma_t'(x)^2}$, a nonlinear PDE on quantile functions

Question

While pondering Wasserstein-2 gradient flows of the Kullback-Leibler divergence functional $\text{KL}(\cdot \mid \nu)$, where $\nu \sim \mathcal N(0, 1)$ is the standard normal distribution (yes, I know about Langevin dynamics and Fokker-Planck, but I am coming to this from a different angle), I arrived at the following second order nonlinear PDE on quantile functions: \begin{equation} \label{eq:1} \tag{$\star$} \partial_t \gamma_t(x) = - \gamma_t(x) + \frac{\gamma_t''(x)}{\gamma_t'(x)^2}, \qquad \forall x \in (0, 1), \ \forall t > 0 \end{equation} with some initial condition $\gamma_0(x) = f(x)$, where $f$ is a quantile function of a probability measure on $\mathbb R$, e.g. $f(x) = \ln\left(\frac{x}{1-x}\right)$, which is the quantile function of a logistic distribution.

I am trying to solve this equation or at least "get a feel" for it.

Edit

Through the connection with W2-gradient flows of the KL-divergence I am relatively sure that the densities $p_t := (\gamma_t^{-1})'$ must fulfill the Fokker-Planck equation $\partial_t p_t(x) = \Delta p_t(x) + x \cdot \nabla p_t(x) + p_t(x)$, but I don't know how to prove this connection.

In particular, if I did everything right in deriving this equation (which I am not sure about at all), then $\gamma_t$ should tend, for $t \to \infty$, to the quantile function of the standard normal distribution $\mathcal N(0, 1)$ and if the initial condition is the quantile function of a normal distribution, $\gamma_t$ should remain the quantile function of some normal distribution for all $t \ge 0$.

The following is a plot the evolution for the above mentioned initial condition, but the simulation breaks down for $t > \frac{1}{2}$.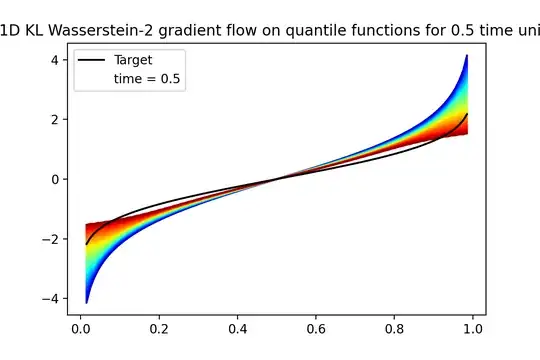

Ideas

• The steady-state solution of \eqref{eq:1}, that is, the solution to $- \gamma(x) + \frac{\gamma''(x)}{\gamma'(x)^2}$ is $\gamma(x) = \sqrt{2} \text{erf}^{-1}\left( \sqrt{\frac{2}{\pi}} c_1 (x + c_2) \right)$.
• I tried taking the Fourier transform (with respect to $x$) of \eqref{eq:1}, but I couldn't handle the term $\frac{\gamma_t''(x)}{\gamma_t'(x)^2} = - \frac{d}{d x} \frac{1}{\gamma_t'(x)}$.
• Looking for invariants of \eqref{eq:1}, I noticed that if $\gamma$ solves the equation, then neither $\gamma + a$, $a \cdot \gamma$, $\frac{1}{\gamma}$ nor $(t, x) \mapsto \gamma_t(1 - x)$ solve \eqref{eq:1}, where $a \in \mathbb R$ is a constant.
• The separable ansatz $\gamma_t(x) = T(t) X(x)$ leads to $T'(t) T(t) + T(t)^2 = \frac{X''(x)}{X'(x)^2 X(x)}$ if $X(x) \ne 0$, so that we have $T'(t) T(t) + T(t)^2 = \lambda$ and $X''(x) = \lambda X'(x)^2 X(x)$ for some constant $\lambda \in \mathbb R$. Hence $T(t) = \pm \sqrt{e^{C_1 - 2 t} + \lambda}$ and $X(x) = \sqrt{\frac{2}{\lambda}} \text{erf}^{-1}\left(\sqrt{\lambda} \tilde{c_1} (x + c_2) \right)$.
• The separable ansatz $\gamma_t(x) = T(t) + X(x)$ yields $T'(t) = - T(t) - X(x) + \frac{X''(x)}{X'(x)^2}$ and thus $T'(t) + T(t) = \lambda$ and $\frac{X''(x)}{X'(x)^2} = \lambda + X(x)$ and thus $T(t) = c_1 e^{-t} + \lambda$ and $X(x) = \sqrt{2} \text{erf}^{-1}\left(\tilde{c_1} e^{-\frac{1}{2} \lambda^2} (c_2 + x)\right) - \lambda$, which leads to the IMO "nicer" $$ \gamma_t(x) = c_1 e^{-t} + \sqrt{2} \text{erf}^{-1}\left(\tilde{c_1} e^{-\frac{1}{2} \lambda^2} (c_2 + x)\right). $$

These two ansatz generate families of solutions. Are those all the solutions?

Answer 1

Since it seems that $\gamma_t'$ is sometimes (always?) positive, it may be possible to invert, and let me denote $\gamma_t$ as $u(x,t)$, as $$ x = r(u,t). $$ If so, the equation $u_t+u=\frac{u_{xx}}{u_x^2}$ (subscripts now denoting derivatives) linearizes as $$ r_t = u r_u+r_{uu}. $$ That has a lot of solutions, but I have not tried to see how they might relate to the separable ones that you have given.