0

I'm interested in running simulations with multivariate normal distributions in which the covariance matrix A has diagonal entries $a_{ii}=1$ and off-diagonal entries $|a_{ij}|<1,i\neq j$. There are two conditions for a matrix to qualify as a covariance matrix: It must be symmetric and positive definite. The first is trivial to arrange; but the second not so much.

To build some intuition, I considered low-dimensional cases. In 2 dimensions, the matrix is always positive definite because $[[1,a],[a,1]]$ is positive definite whenever $|a|<1$.

In 3 dimensions, I wrote a simple Python program to generate 1 million suitable positive definite matrices.

def generate_data(n,dim):
    def generate_covariance():
        posdef=False
        while posdef==False:
            covariance=np.empty([dim,dim])
            for i in range(dim):
                for j in range(i,dim):
                    if i==j:
                        covariance[i][j]=1
                    else:
                        covariance[i][j]=np.random.uniform(low=-1,high=1)
                for j in range(i):
                    covariance[i][j]=covariance[j][i]
            posdef=np.all(np.linalg.eigvals(covariance)>0)
        return covariance
    cov=generate_covariance()
    return cov

xdata=[]
ydata=[]
zdata=[]
for i in range(1000000):
    A=generate_data(1,3)
    xdata.append(A[0][1])
    ydata.append(A[0][2])
    zdata.append(A[1][2])
ax=plt.axes(projection='3d')
ax.scatter3D(xdata,ydata,zdata)
sys.exit()

Here is what the result looks like: 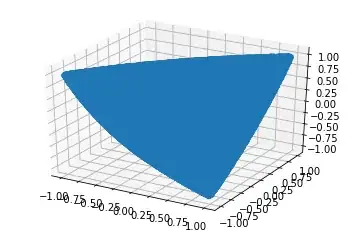enter image description here

This looks like a 2-dimensional region (specifically the region inside a triangle). But I would have expected a 3-dimensional region because there are 3 variables, and the condition that all 3 eigenvalues be positive sounds like it should yield a (complicated) system of inequalities.

Curious, I then modified the code to instead generate 1 million matrices and count how many were positive definite. The answer was 616,734. So the plot was misleading and in fact more than half the matrices are positive definite.

So why is the plot misleading? What should it actually look like? What can we say about higher dimensional cases? (I know from counting 7x7 matrices that positive definite matrices are much rarer than 1/2^7, but can we say more?)

And my original thought/question: Can I modify the code to generate positive definite matrices more often (in higher dimensions), while still getting a decently representative sample of all possible positive definite matrices?

Thanks

Rodrigo de Azevedo
  • 23,223
J.D.
  • 93

3 Answers3

1

Devroye, L. and Letac, G. (2010) 'Copulas in $3$ dimensions with prescribed correlations.' https://arxiv.org/abs/1004.3146

Gerry Myerson
  • 185,413
Gérard Letac
  • 4,542
0

In three dimensions, your matrix is $$ \pmatrix{1&a&b\cr a&1&c\cr b&c&1\cr} $$ with determinant $$ 1+2abc-a^2-b^2-c^2 $$ which is negative (thus making the matrix not positive definite) whenever two of the numbers $a,b,c$ are big enough that their squares add up to more than $1$, and the third number is small enough that $2abc$ doesn't compensate.

E.g., one can work out that if $a=b=0.8$ then the determinant is negative for $c<0.28$.

Gerry Myerson
  • 185,413
0

Re my last question, I think I found a decent answer: Sylvester's criterion. A symmetric $n\times n$ matrix is positive definite if and only if for $i\leq n$, the determinant of the top-left $i\times i$ submatrix ix positive. So what I could do is start with the $1\times 1$ identity matrix, and inductively expand by 1 row & column at a time, filling in the new entries randomly, and redoing that until the new $(i+1)\times (i+1)$ matrix has positive determinant.

J.D.
  • 93