How to evaluate $\displaystyle \int_{-\pi/2}^{\pi/2} f(x) dx$ where $f(x)=\cos(x)+\sin(f(x))$

Question

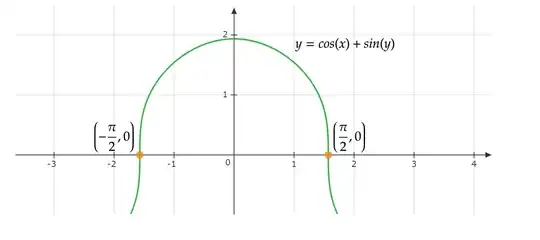
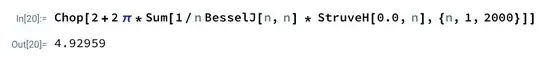So I want to find the area of this circular looking thing.

I had the following thought process in solving it.

Consider the implicit derivative of the function.

$\begin{align} y &= \cos(x)+\sin(y) \\ \mathrm{d}y &= -\mathrm{d}x \sin(x)+\mathrm{d}y \cos(y) \\ \mathrm{d}y (\cos (y) -1) &= \mathrm{d}x \sin (x) \\ \dfrac{\mathrm{d}y}{\mathrm{d}x} &= \dfrac{\sin (x)}{\cos(y)-1} \end{align}$

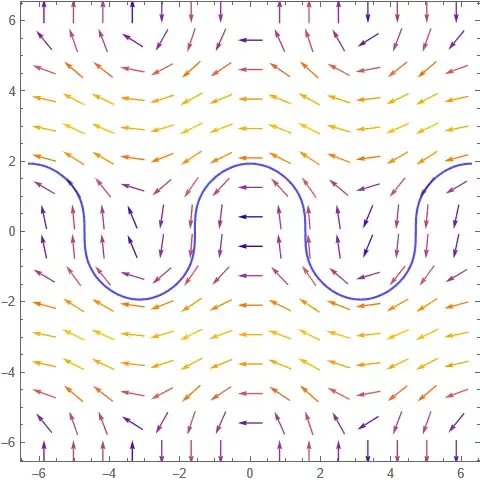
Then consider a parametric equation $r(t)=\begin{bmatrix} x(t) \\ y(t) \end{bmatrix}$ that lines up with the implicit differentiation above i.e. $r'(t)=\begin{bmatrix} x'(t) \\ y'(t) \end{bmatrix}=\begin{bmatrix} \cos(y(t))-1 \\ \sin(x(t)) \end{bmatrix}$. This is what the vector field $\begin{bmatrix} x \\ y \end{bmatrix} \to \begin{bmatrix} \cos(y)-1 \\ \sin(x) \end{bmatrix}$ looks like superimposed on the graph.

The derivative vectors go anticlockwise relative to the graph, which gave me an idea. Take Green's theorem: $\displaystyle \oint_C \vec{F} \cdot \vec{dr} = \iint_R \nabla \times \vec{F} dA$ and apply it to this problem in an interesting fashion.

If $\vec{F}(x,y) = \begin{bmatrix}0\\x\end{bmatrix}$, then $\nabla \times \vec{F} = 1$ which means I can use the line integral to calculate the area. I should maybe point out that this is 2D curl, which in 3D would technically be $\hat{k}$.

I got stuck at this assortment of half-ideas. Of course I can write the equation in terms of x like this: $f(y) = \cos^{-1} (y - \sin(y))$, do approximations to get the upper y bound at the crest of the thing like this: $a = \cos(0) + \sin(a) \implies a = 1 + \sin a$ then approximate an integral to get the answer like this: $\text{Area} = 2\displaystyle \int_0^a \cos^{-1} (y - \sin(y)) \mathrm{d}y$, which gives me this answer to several decimal places: $4.9296448613689990829170456909320900725529417147308463240261037884$.

But that's boring. Is there any other way?

Answer 1

$\def\J{\operatorname J} \def\H{\operatorname H} $ Apply the Kepler equation Fourier series, so Bessel J appears

$$\text{Area}=\int_{-\frac\pi2}^\frac\pi2\cos(x)+\sum_{n=1}^\infty\frac{2\sin(n\cos(x))}{n}\J_n(n)dx= 2+\sum_{n=1}^\infty \frac{2\J_n(n)}n\int_{-\frac\pi2}^\frac\pi2\sin(n\cos(x))dx $$

The integral is Struve H. Therefore:

$$\boxed{\text{Area}=2+2\pi\sum_{n=1}^\infty\frac{\J_n(n)\H_0(n)}n}$$

which is a Kapteyn series with $a_n=\frac{\H_0(n)}n$ and seemingly no closed form. Mathematica shows this series numerically matches the area despite fairly slow convergence: