2

This question is motivated by a self-supervised learning problem in machine learning, but I'll try to strip out as many unnecessary details as possible. In this setting, we have large datasets and we constrain our deep neural network's outputs to lie on the hypersphere. I'm curious to know the spectral behavior of the network's outputs.

Suppose I have $N$ points drawn uniformly at random from the hypersphere in $D$ dimensions. If I form a $N \times D$ matrix of the points, what can I say about the matrix's singular values? In the limit as $N\rightarrow \infty$, do the singular values have a limiting distribution?

Rylan Schaeffer
  • 544
  • 1
    Are you mostly interested in the largest SV? For $D=2$ I seem to have got $\sigma_1 / \sqrt{N} \to \sqrt{\pi}$. For other dim the intuition is simple i.e. $\sigma_1 / \sqrt{N}$ should converge to $\sqrt{\Bbb E((x^Te_1)^2, x\in\Bbb S^{D-1})}, |e_1|=1$ but the exact value might be complicated. – Vim Jul 12 '23 at 16:29
  • 1
    The intuition is that, when $N$ is large, the points $x_i$ should be very uniform across $\Bbb S^{D-1}$. Recall the fact that $\sigma_1$ is the operator norm of the $N\times D$ matrix (say $M$ whose row vectors are $x_i$). So we search for the unit vector $e$ that maximises $|Me|=\sqrt{\sum_i (x_i^Te)^2}$. But since for large $N$, $x_i$ are uniformly distributed, it follows that the direction of $e$ doesn't quite matter, and the equation under the square root when divided by $N$ is just the surface integral $\int (x^Te_1)^2 d|\Bbb S^{D-1}|$ where $x$ ranges uniformly over $\Bbb S^{D-1}$. – Vim Jul 12 '23 at 16:39
  • 1
    Actually by this rationale even the other SVs should also converge to the exact same value as $\sigma_1$ do when divided by $\sqrt{N}$ because they can be also defined in the operator norm manner... I can't run a large enough numerical experiment right now because memory would run out when SVD is performed for $N > 10000$. Hopefully someone on this side can verify/falsify my above results numerically. – Vim Jul 12 '23 at 16:48
  • 1
    Per my first comment: sorry I seem to have forgot the normalising factor $2\pi$ for $D=2$ (i.e. $|\Bbb S^1|$), so the result should be $\sigma_1/\sqrt{N}\to \sqrt{\pi/2\pi}=\sqrt{1/2}$ instead. And in my second comment, the surface integral $\int (x^Te_1)^2 d|\Bbb S^{D-1}|$ should be divided by the normalising constant $|\Bbb S^{D-1}|$ too otherwise it won't equal $\Bbb E((x^Te_1)^2, x\in\Bbb S^{D-1})$ – Vim Jul 13 '23 at 00:56
  • I'm confused by the reason that the direction of $e$ doesn't matter once considering the 2nd, 3rd and so on singular values. Yes, for the first, I agree the direction doesn't matter, but once the 1st singular direction is chosen and the data projected to one dimension lower, the remaining dimensions are no longer uniform on the sphere, I would think? – Rylan Schaeffer Jul 14 '23 at 02:31
  • You can check in my answer that the convergence in probability is uniform w.r.t. the choice of $e$, regardless of which subspace they are picked from. – Vim Jul 14 '23 at 03:53
  • In other words all $|Me|/\sqrt N, \forall |e|=1$ converge to exactly the same value and at the same speed (or more rigorously, no slower than a uniform speed). And each SV is just one possible value of $|Me|$ for some $e$. – Vim Jul 14 '23 at 04:00
  • I might be misunderstanding, but I think your answer assumes that the data $x_i$ are uniform on the hypersphere. What I'm confused by is that (at least inso far as I understand) this assumption doesn't seem valid after the 1st singular direction has been identified? – Rylan Schaeffer Jul 15 '23 at 17:09
  • Please refer to this page. Whichever SV only depends on $M$, and $M$ remains the same. True, the second SV and so on is restricted to picking $e$ from lower dimensional subspaces, but that doesn't change $M$ itself. If $|Me|$ is the same for all $e$, it doesn't matter at all which subspace $e$ is picked from because it's the same constant all along. – Vim Jul 15 '23 at 17:43
  • Also it seems weird to say we pick the second SV after the first SV. The two processes can happen completely independently of each other? – Vim Jul 15 '23 at 17:53
  • 1
    As a completely irrelevant sidenote, I really like the jokes on your personal homepage. – Vim Jul 16 '23 at 05:49

1 Answers1

1

Define the $N\times D$ matrix as $M$, then we have $$\sigma_k(M)/\sqrt{N} \overset{\Bbb P}{\to} \sqrt{\Bbb E((x^Te_1)^2)}$$ where $\Bbb E((x^Te_1)^2)$ is a constant and can be easily estimated by Monte Carlo.

Proof:

Suppose $M$'s row vectors are $x_i\in\Bbb S^{D-1}$, fix an arbitrary $e\in\Bbb S^{D-1}$, and let $$\mu:=\Bbb E((x^Te_1)^2),\quad v:=\Bbb V((x^Te_1)^2)$$ where $x$ follows the uniform distribution on $\Bbb S^{D-1}$. Note that $\mu(e), v(e)$ actually don't depend on $e$ so we may just write it as $\mu, v$. By Chebyshev, we have $$\Bbb P\left(\left|\frac1N\sum_{i=1}^N(x_i^Te)^2-\mu\right| > \epsilon\right) \le \frac{v}{N\epsilon^2}$$ Therefore $\sqrt{\frac1N\sum_{i=1}^N(x_i^Te)^2}\overset{\Bbb P}{\to}\sqrt\mu$ uniformly for each $e$. This completes the proof, recalling the fact that all SVs can be defined as operator norms.

My Monte Carlo results for $D=3$:

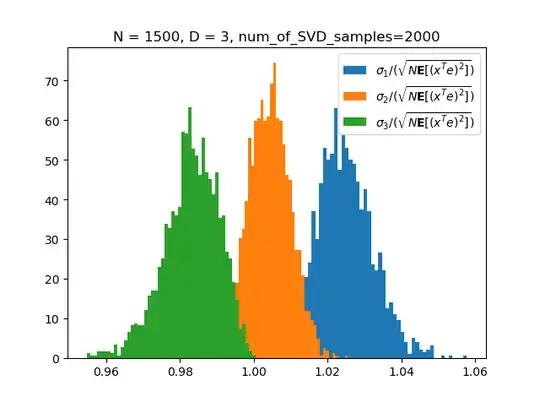
enter image description here

Code:

import numpy as np
import matplotlib.pyplot as plt

def sample_spherical(npoints, ndim=3):
    vec = np.random.randn(ndim, npoints)
    vec /= np.linalg.norm(vec, axis=0)
    return vec


def get_sqrt_expectation_in_nD(ndim):
    unit_vec = np.array([[1] + [0] * (ndim - 1)])
    vec = sample_spherical(10000, ndim)
    return (((unit_vec @ vec) ** 2)[0].mean()) ** 0.5


def plot_distribution(nsamples, npoints, ndim=3):
    sv_samples = np.zeros((nsamples, ndim))
    for i in range(nsamples):
        a = sample_spherical(npoints, ndim)
        , s, _ = np.linalg.svd(a)
        sv_samples[i] = s
    expec = get_sqrt_expectation_in_nD(ndim)
    sv_samples /= expec * np.sqrt(npoints)
    for k in range(ndim):
        plt.hist(sv_samples[:, k], cumulative=False, density=True, bins=50,
                 label=r"$\sigma{%d}/(\sqrt{N{\bf{E}}[(x^Te)^2]})$" % (k + 1))
        pass
    plt.legend()
    plt.title("N = %d, D = %d, num_of_SVD_samples=%d" % (npoints, ndim, nsamples))
    return sv_samples


samples = plot_distribution(2000, 1500, 3)
Vim
  • 13,905
  • Hi Vim, thanks for your answer! Give me a day or two to think over your answer before I decide whether it answers the question. In the interim, don't the Monte Carlo simulations suggest the opposite? Those look like 3 pretty clearly distinguished clusters with decreasing centroids. – Rylan Schaeffer Jul 14 '23 at 02:28
  • 1
    Actually all 3 clusters are very close to 1. The reason they look distinguished from each other is N and num_SV_samples are too small. If you have sufficient computational resources, I would suggest you set larger values of these and check if the clusters are, well, more "clustered" together. – Vim Jul 14 '23 at 03:52