Their formula
$$
\frac{\partial\hat{\boldsymbol{k}}}{\partial t}=\boldsymbol{\omega}\times\hat{\boldsymbol{k}}
$$
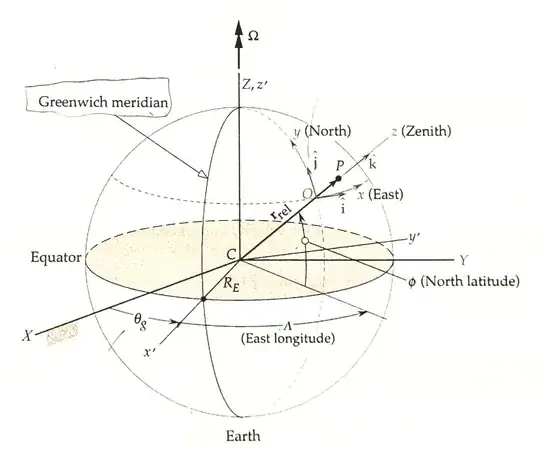
indicates that $\boldsymbol{\omega}$ is the spin angular velocity
of the radial unit vector $\hat{\boldsymbol{k}}$ that moves when
latitude and longitude relative to earth change with time.
I prefer to use a more standard notation for spherical polar coordinates:
- $r$ radius,
- $\phi$ east longitude (your $\Lambda$),
- $\theta$ zenith angle ($\pi/2$ minus north latitude, your $\phi$)
- $\hat{\boldsymbol{r}},\hat{\boldsymbol{\theta}},\hat{\boldsymbol{\phi}}$ for your unit basis vectors $\hat{\boldsymbol{k}},\hat{\boldsymbol{j}},\hat{\boldsymbol{i}}$
The conversion between the Cartesian and polar basis vectors is
$$
\begin{bmatrix}\hat{\boldsymbol{r}}\\\hat{\boldsymbol{\theta}}\\\hat{\boldsymbol{\phi}}\end{bmatrix}=
\begin{bmatrix}
\sin\theta\cos\phi&\sin\theta\sin\phi&\cos\theta\\
\cos\theta\cos\phi&\cos\theta\sin\phi&-\sin\theta\\
-\sin\phi &\cos\phi & 0
\end{bmatrix}
\begin{bmatrix}\hat{\boldsymbol{x}}\\\hat{\boldsymbol{y}}\\\hat{\boldsymbol{z}}\end{bmatrix}\,.
$$
Therefore your $\displaystyle\frac{\partial\hat{\boldsymbol{k}}}{\partial t}$ is
\begin{align}
\dot{\hat{\boldsymbol{r}}}&=\Big(\dot\theta\cos\theta\cos\phi-\dot\phi\sin\theta\sin\phi\Big)\hat{\boldsymbol{x}}+\Big(\dot\theta\cos\theta\sin\phi+\dot\phi\sin\theta\cos\phi\Big)\hat{\boldsymbol{y}}-\dot\theta\sin\theta\,\hat{\boldsymbol{z}}\\
&=\dot\theta\,\hat{\boldsymbol{\theta}}+\dot\phi\,\sin\theta\,\hat{\boldsymbol{\phi}}\,.
\end{align}
Since $\sin\theta$ is $\cos(\theta-\pi/2)=\cos(\pi/2-\theta)$ this is
the same equation that they have in their notation.
Their angular velocity is in my notation
$$
\boldsymbol{\omega}=\dot\theta\hat{\boldsymbol{\phi}}\color{red}{-}\dot\phi\,\sin\theta\,\hat{\boldsymbol{\theta}}
+\dot\phi\,\cos\theta\,\hat{\boldsymbol{r}}\,.
$$
Note that their $-\dot\phi$ becomes $\dot\theta$ because they measure the zenith angle
from the equator instead of the north pole. (They seem however to have
a sign error in front of the $\hat{\boldsymbol{\theta}}$ term.)
The verification that this angular velocity satisfies
$$\tag{1}
\dot{\hat{\boldsymbol{r}}}=\boldsymbol{\omega}\times \hat{\boldsymbol{r}}
$$
is quite simple when one uses the relationships
$$\boxed{\quad\phantom{\Bigg|}
\hat{\boldsymbol{r}}\times\hat{\boldsymbol{\theta}}=\hat{\boldsymbol{\phi}}\,,\quad
\hat{\boldsymbol{\theta}}\times\hat{\boldsymbol{\phi}}=\hat{\boldsymbol{r}}\,,\quad
\hat{\boldsymbol{\phi}}\times\hat{\boldsymbol{r}}=\hat{\boldsymbol{\theta}}\,.\quad}
$$
Since I have seen people being baffled about the correctness
of those let's prove them:
\begin{align}\require{cancel}
\hat{\boldsymbol{r}}\times\hat{\boldsymbol{\theta}}&=\Big(\cancel{\sin\theta\cos\phi\cos\theta\sin\phi}-\cancel{\cos\theta\cos\phi\sin\theta\sin\phi}\Big)\,\underbrace{\hat{\boldsymbol{x}}\times\hat{\boldsymbol{y}}}_{\textstyle\hat{\boldsymbol{z}}}\\
&~-\Big(\sin^2\theta\sin\phi+\cos^2\theta\sin\phi\Big)\,\underbrace{\hat{\boldsymbol{y}}\times\hat{\boldsymbol{z}}}_{\textstyle\hat{\boldsymbol{x}}}\\
&~+\Big(\sin^2\theta\cos\phi+\cos^2\theta\cos\phi\Big)\,
\underbrace{\hat{\boldsymbol{z}}\times\hat{\boldsymbol{x}}}_{\textstyle\hat{\boldsymbol{y}}}\\
&=-\sin\phi\,\hat{\boldsymbol{x}}+\cos\phi\,\hat{\boldsymbol{y}}\\
&=\hat{\boldsymbol{\phi}}\,,\\[2mm]
\hat{\boldsymbol{\theta}}\times\hat{\boldsymbol{\phi}}&=\Big(\cos\theta\cos^2\phi+\cos\theta\sin^2\phi\Big)\,\underbrace{\hat{\boldsymbol{x}}\times\hat{\boldsymbol{y}}}_{\textstyle\hat{\boldsymbol{z}}}+\sin\phi\sin\theta\,\underbrace{\hat{\boldsymbol{z}}\times\hat{\boldsymbol{x}}}_{\textstyle\hat{\boldsymbol{y}}}
-\sin\theta\cos\phi\,\underbrace{\hat{\boldsymbol{z}}\times\hat{\boldsymbol{y}}}_{\textstyle-\hat{\boldsymbol{x}}}\\
&=\hat{\boldsymbol{r}}\,,\\[2mm]
\hat{\boldsymbol{\phi}}\times\hat{\boldsymbol{r}}&=-\Big(\sin\theta\cos^2\phi+\sin\theta\sin^2\phi\Big)\,\underbrace{\hat{\boldsymbol{x}}\times\hat{\boldsymbol{y}}}_{\textstyle\hat{\boldsymbol{z}}}-\sin\phi\cos\theta\,\underbrace{\hat{\boldsymbol{x}}\times\hat{\boldsymbol{z}}}_{\textstyle-\hat{\boldsymbol{y}}}
+\cos\theta\cos\phi\,\underbrace{\hat{\boldsymbol{y}}\times\hat{\boldsymbol{z}}}_{\textstyle\hat{\boldsymbol{x}}}\\
&=\hat{\boldsymbol{\theta}}\,.
\end{align}
Remark.
One thing I don't understand though is where the $\hat{\boldsymbol{r}}$-component in their angular velocity comes from. It has obviously no
influence on the validity of the equation (1). Also, if we drop it
it is easiy to see that the angular velocity becomes equal to the
orbital angular velocity
$$
\boldsymbol{\omega}=\hat{\boldsymbol{r}}\times \dot{\hat{\boldsymbol{r}}}\,.
$$