0

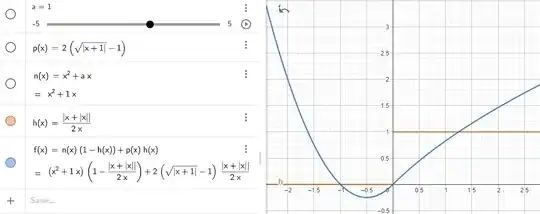
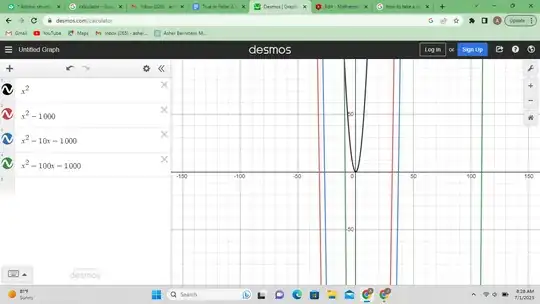
I want to tell a statistical programm to draw a graph represneting a general concept so I don't have data. I want that my function is in the beginning quadratic with positive sign at x^2 and then starts increasing and is concave. I had such things in high-school and totally forgot how the general formula for such a function would look like.

Thank you in advance for your help

Emilia
  • 67

3 Answers3

1

Here is a solution illustrated by a Geogebra graphics :

enter image description here

using the so-called "Heaviside function"

$$h(x)=\frac{x+|x|}{2x}=\begin{cases}0& \text{if} \ x<0\\1& \text{if} \ x>0\end{cases}$$ (graphical representation in red) ;

$j(x)=1-h(x)$ has the inverse behavior.

Therefore, writing :

$$f(x)=(1-h(x))n(x)+h(x)p(x)=\begin{cases}n(x)& \text{if} \ x<0\\p(x)& \text{if} \ x>0\end{cases}$$

where $n(x)$ is for the negative part, and $p(x)$ the positive part.

(I have chosen the positive part in such a way that the connection in $0$ is smooth).

Is it what you wanted ?

Jean Marie
  • 88,997
0

I don't believe that it is possible to create a concave function with a positive $x^2$ term at the beginning if it's quadratic. If a quadratic has a positive $x^2$ term, it will always be convex. To prove this, start by looking at the function $x^2$. This function opens upward and is convex. Now, graph $x^2 - 1000$. All this does is bring $x^2$ down by $1000$, so it's still convex. Now, graph $x^2 - 10x - 1000$. This moves the function to the right, which still makes it convex. Finally, if you graph any crazy numbers, such as $x^2 - 10000x - 10000$, you will see that the function is still convex. Here's the graph: enter image description here

Itoz Darbien
  • 474
Berny
  • 66
  • 1
    As it’s currently written, your answer is unclear. Please [edit] to add additional details that will help others understand how this addresses the question asked. You can find more information on how to write good answers in the help center. – Community Jul 01 '23 at 12:18
  • Sure. I'll do that – Berny Jul 01 '23 at 12:19
  • 1
    It is not necessary to take so many examples $f(x)=x^2+bx+c$ is convex because plainly its second derivative $2$ is ("always") $>0$. – Jean Marie Jul 01 '23 at 13:14
  • I know. I just put many examples to show that a concave function with an x^2 term is not possible and to make it easier to understand. – Berny Jul 01 '23 at 13:41
0

In fact, a quadratic function with a positive $x^2$ term will be convex.

Let $f(x)=ax^2+bx+c(a>0)$, which satisfies your demand.

Then $f'(x)=2ax+b,f''(x)=2a>0$. So $f(x)$ is a convex function.

You can read this Wiki

Itoz Darbien
  • 474