An integral identity: $\int_{0}^{\large\frac{π}{2}}\dfrac{\cos^{a}x\sin(a+1)x}{\sin x}\ \mathrm{d}x$

Question

I recently came across a parametric definite integral about Chebyshev polynomials:

$$ f(a)= \begin{aligned} \begin{gather*} \int_{0}^{\frac{\pi}{2}}\dfrac{\cos^{a}x\sin(a+1)x}{\sin x}\ \mathrm{d}x \end{gather*} \end{aligned} $$

Easily, I found out the form of Chebyshev polynomials of the Second kind and guessed that the integration result might be a constant or something.

We know that Chebyshev polynomials of the Second kind satisfies the following differential equation: $$ \begin{aligned} \begin{gather*} (1-x^2)\ U''_{a}(x)-3x\ U_{a}'(x)+a(a+2)\ U_{a}(x)=0 \end{gather*} \end{aligned} $$

Let $\ \displaystyle U_{a}(x)=\sum_{k=0}^{\infty}{u_{k}\ x^k}$, we can get that $\displaystyle u_{k+2}=\dfrac{(k-a)(k+a+2)}{(k+1)(k+2)}u_{k}$, which means that $$ \begin{aligned} \begin{gather*} \displaystyle U_{a}(x)=\sum_{k=0}^{\infty}{\dfrac{(-2)^k\ \Gamma\left({\large\frac{k+a}{2}}+1\right)\Gamma\left({\large\frac{k-a}{2}}\right)}{\Gamma(k+1)}x^k} \end{gather*} \end{aligned} $$

MeanWhile，$$ \begin{aligned} \begin{gather*} \displaystyle \int_{0}^{1}{\dfrac{x^u}{\sqrt{1-x^2}}\ \mathrm{d}x}=\dfrac{\sqrt{π}\ \Gamma({\large\frac{u+1}{2}})}{2\ \Gamma({\large\frac{u}{2}}+1)},\ u>-1 \end{gather*} \end{aligned} $$

Finally, it ends up with one series following: $$ \begin{aligned} \begin{gather*} -\dfrac{\sin(πa)}{2π}\sum_{k=0}^{\infty}{\dfrac{\sqrt{π}\ (-2)^k\ \Gamma\left({\large\frac{k-a}{2}}\right)\Gamma\left({\large\frac{k+a+1}{2}}\right)}{2\ \Gamma(k+1)}} \end{gather*} \end{aligned} $$

I have been going at this Series all day and I am confused on where to begin.Thoughts and several Solution ideas are greatly appreciated !

Answer 1

For convenience let's rewrite the integral as $$f(a)= \int_{0}^{\pi/2} \cos^{a-1}(x) \frac{\sin(ax)}{\sin x} \, \mathrm dx. $$

Then assuming that $a>0$, we have

$$ \begin{align} f(a) &= \int_{0}^{\pi/2} \cos^{a-1}(x) \frac{\sin(ax)}{\sin x} \, \mathrm dx \\ &\overset{(1)}{=} \int_{0}^{\infty} \frac{1}{(1+u^{2})^{a/2}} \, \frac{\sin \left(a \arctan u \right)}{u} \, \mathrm du \\ &\overset{(2)}{=} \int_{0}^{\infty}\frac{1}{(1+u^{2})^{a/2}} \frac{1}{u} \frac{(1+u^{2})^{a/2}}{\Gamma(a)} \int_{0}^{\infty} e^{-t} \sin(ut) t^{a-1} \, \mathrm dt \, \mathrm du \\ &= \frac{1}{\Gamma(a)} \int_{0}^{\infty} \frac{1}{u} \int_{0}^{\infty} e^{-t} \sin(ut) t^{a-1} \, \mathrm dt \, \mathrm du \\ &= \frac{1}{\Gamma(a)}\lim_{b \to \infty} \int_{0}^{b} \frac{1}{u} \int_{0}^{\infty} e^{-t} \sin(ut) t^{a-1} \, \mathrm dt \, \mathrm du \\ &\overset{(3)}{=} \frac{1}{\Gamma(a)} \lim_{b \to \infty} \int_{0}^{\infty} t^{a-1}e^{-t} \int_{0}^{b} \frac{\sin(tu)}{u} \, \mathrm du \, \mathrm dt \\ &=\frac{1}{\Gamma(a)} \lim_{b \to \infty} \int_{0}^{\infty} t^{a-1} e^{-t} \operatorname{Si}(bt)\, \mathrm dt \\ &= \frac{1}{\Gamma(a)} \int_{0}^{\infty}\lim_{b \to \infty}t^{a-1} e^{-t} \operatorname{Si}(bt) \, \mathrm dt \\ &\overset {(4)}{=} \frac{1}{\Gamma(a)} \frac{\pi}{2} \int_{0}^{\infty} t^{a-1} e^{-t} \, \mathrm dt \\ &= \frac{\pi}{2}. \end{align}$$

---

$(1)$ Let $u = \tan(x)$.

$(2)$ Prove that $\int_{0}^{+\infty} u^{s-1} \cos (a u) \:e^{-b u}\:du=\frac{\Gamma(s)\cos\left(s\arctan \left(\frac{a}{b}\right)\right)}{(a^2+b^2)^{s/2}}$

$(3)$ Fubini's theorem

$(4)$ Since $|\operatorname{Si}(t)|$ is a bounded by a constant for all $t \in \mathbb{R}$, the dominated convergence theorem permits us to bring the limit inside the integral.

---

Old answer:

We can use contour integration to show that $f(a)=\frac{\pi}{2}$ for all $a >-1$.

Using the principal branch of the logarithm, we have

$$ \begin{align} f(a) &= \frac{1}{2} \int_{-\pi/2}^{\pi/2} \frac{\cos^{a}(x) \sin \left((a+1)x\right)}{\sin(x)} \, \mathrm dx \\ &= \frac{1}{2} \, \Im \, \operatorname{PV} \int_{-\pi/2}^{\pi/2} \frac{\cos^{a}(x)e^{i(a+1)x}}{\sin(x)} \, \mathrm dx \\ &= \frac{1}{2} \, \Im \, \operatorname{PV} \int_{-\pi/2}^{\pi/2} \frac{ \left(\frac{e^{ix}+e^{-ix}}{2} \right)^{a}e^{i(a+1)x}}{\frac{e^{ix}-e^{-ix}}{2i}} \, \mathrm dx \\ &= \frac{1}{2^{a}} \, \Im \, \operatorname{PV} \, \int_{C} \frac{\left(z+ \frac{1}{z} \right)^{a}z^{a+1}}{z- \frac{1}{z}} \frac{\mathrm dz}{z} \\ &= \frac{1}{2^{a}} \, \Im \, \operatorname{PV} \int_{C} \frac{z\left(z^{2}+ 1 \right)^{a}}{z^{2}-1} \, \mathrm dz, \end{align}$$

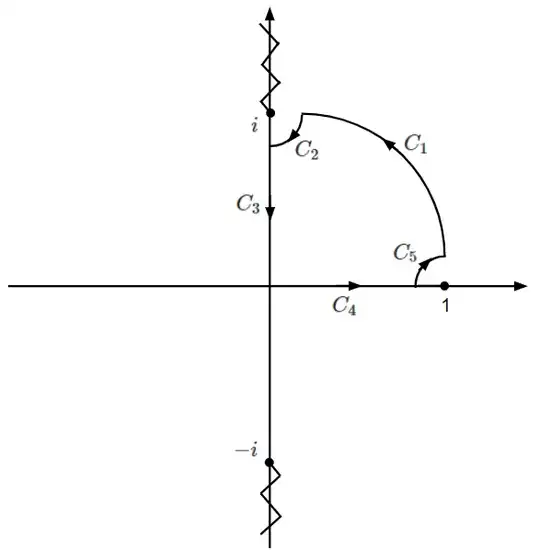
where $C$ is the right half of the unit circle indented at $z=1$, $z=i$ and $z=-i$.

The singularity at $z=1$ is a simple pole, while the singularities at $z=i$ and $z=-i$ are branch points.

The branch cuts for $(z^{2}+1)^{a}$ are on $(-i \infty, -i]$ and $[i, i \infty)$.

Closing the contour along the imaginary axis and letting the radii of the indentations go to zero, we get $$\operatorname{PV} \int_{C} \frac{z(z^{2}+1)^{a}}{z^{2}-1} \, \mathrm dz - i \pi \operatorname{Res} \left[\frac{z(z^{2}+1)^{a}}{z^{2}-1}, z=1\right] - \int_{-1}^{1} \frac{t(1-t^{2})^{a}}{1+t^{2}} \, \mathrm dt = 0. $$

(The contributions form the indentations at $z=i$ and $z=-i$ vanish since $\lim_{ z \to \pm i}(z \pm i)\frac{z(z^{2}+1)^{a}}{z^{2}-1} =0 $.)

Equating the imaginary parts on both sides of the above equation, we have $$ \Im \, \operatorname{PV} \int_{C} \frac{(z^{2}+1)^{a}}{z^{2}-1} \, \mathrm dz = \pi \operatorname{Res} \left[\frac{z(z^{2}+1)^{a}}{z^{2}-1}, z=1\right] = \pi \, 2^{a-1}.$$

Therefore, $$f(a) = \frac{1}{2^{a}} \left(\pi \, 2^{a-1} \right) = \frac{\pi}{2}.$$

Answer 2

We can generalize the OP as

$$I=\int_{0}^{\frac{\pi}{2}}\dfrac{\cos^{a}(x)\sin(a+\color{red}k)x}{\sin x}\ dx =\frac\pi2,~~~~a>-1\land \color{red}k=1,3,5,\dots$$

Let $z=e^{ix}$, and choose the following contour

Note that $\cos(x)=\frac12(z+\frac1z),~ \sin(x)=\frac1{2i}(z-\frac1z),~dx=\frac1{iz}~dz$, we get $$I=\Im\int_{0}^{\frac{\pi}{2}}\dfrac{\cos^{a}(x) \cdot e^{i(a+k)x}}{\sin x}\ dx=\frac2{2^a}\Im \int_{C_1}g(z)\ dz\tag{1} $$

where $\displaystyle g(z)=\frac{(z^2+1)^az^k}{z^2-1}$, hence

$$\int_{C_1}+\int_{C_2}+\dots+\int_{C_5}g(z)\ dz=0\tag{2}$$

The integral $\int_{C_2} g(z)\ dz=0$ for $a>-1$. On $C_3$, $z=re^{i\frac\pi2}$, we get

$$\int_{C_3} g(z)\ dz=\int_1^0\frac{(1-r^2)^a\cdot r^k\cdot i^k}{-r^2-1}i\ dr=(-1)^{\frac{k+1}2}\int_0^1\frac{(1-r^2)^a\cdot r^k}{r^2+1}\ dr$$

On $C_4$, $z=x$, we get

$$\int_{C_4} g(z)\ dz=-\int_0^1\frac{(1+x^2)^a\cdot x^k}{1-x^2}\ dx$$

On $C_5$, we get

$$\int_{C_5} g(z)\ dz=-\frac14\cdot 2\pi i \cdot \text{Res}(g(z), z=1)=-\frac\pi2 \cdot \frac{2^a}{2}\cdot i$$

Use eq.(2), we get

$$\int_{C_1}g(z)\ dz+(-1)^{\frac{k+1}2}\int_0^1\frac{(1-r^2)^a\cdot r^k}{r^2+1}\ dr-\int_0^1\frac{(1+x^2)^a\cdot x^k}{1-x^2}\ dx=\frac\pi2 \cdot \frac{2^a}{2}\cdot i$$

Take the imaginary part:

$$\Im\int_{C_1}g(z)\ dz=\frac\pi2 \cdot \frac{2^a}{2}$$

Finally, from eq.(1), we get

$$\boxed{~I=\int_{0}^{\frac{\pi}{2}}\dfrac{\cos^{a}(x)\sin(a+\color{red}k)x}{\sin x}\ dx =\frac\pi2,~~~~a>-1\land \color{red}k=1,3,5,\dots~~}$$

Answer 3

\begin{align} &\int^{\frac{\pi}{2}}_{0} \dfrac{\cos^{a}x\sin(a+1)x}{\sin x}\ dx\\ =& \int^{\frac{\pi}{2}}_{0}\frac{ (e^{i x} + e^{-ix})^{a} \Im e^{i (a+1) x}}{2^a\sin x}dx = \int^{\frac{\pi}{2}}_{0} \frac{ \Im\sum_{k\ge0} \binom {a}k e^{i (2k+1)x}}{2^a\sin x}dx \\ = & \ \sum_{k\ge0}{ \frac{\binom {a}k }{2^a} \int^{\frac{\pi}{2}}_{0}\frac{\sin[(2k+1)x]}{\sin x}dx } = \sum_{k\ge0}\frac{\binom {a}k }{2^a}\frac\pi2 =\frac\pi2 \end{align}