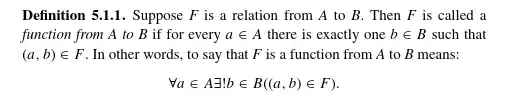0

doesnt $f:\mathbb{R}\to\mathbb{Z}$ mean that $f$ maps every real $x$, to a unique integer $y$? That doesn't imply that that $f$ maps every real $x$, to a unique real $y$, right?

Here is how the book im reading defines a function:

enter image description here

But even if $B\subseteq C$, in my opinion $\forall a\in A\exists!b\in B((a,b)\in F)$ doesn't automatically imply $\forall a\in A\exists!c\in C((a,c)\in F)$

Example: $A=\{1\}$, $B=\{8\}$, $C=\{8,9\}$
$f=\{(1,8),(1,9)\}$

By the definition above, $f:A\to B$, but not $f:A\to C$, even though $B\subseteq C$

lightyourassonfire
  • 355
  • 1
    Wrong. Since $\mathbb Z\subset\mathbb R$, $f$ maps every $x$ to a unique $y\in\mathbb R$. – John Douma Jun 21 '23 at 22:57
  • Does this answer your question? When do two functions become equal? – Joe Jun 21 '23 at 23:17
  • The answer depends on the precise definition of function, as mentioned in the link above. By the way, since every integer is a real number, if $f$ maps every real $x$ to a unique integer $y$, then it is also the case that $f$ maps every real $x$ to a unique real number $y$. (This is true regardless of how you are defining functions precisely.) – Joe Jun 21 '23 at 23:18
  • 1
    What do you mean by "unique"? $f:\mathbb{R}\to\mathbb{Z}$ means that for each real number $x$ there is a single welldefined integer $y$ known as $f(x)$ associated. It does not say that the function is necessarily injective, so the $y$ is not necessarily "unique" in that sense. There could be a distinct real number $x_2$ such that $f(x_2)$ is the same integer $y$ for that one. – Jeppe Stig Nielsen Jun 21 '23 at 23:18
  • @Joe why is it not possible to come up with a function, where every real $x$ is mapped to a unique integer $y$, but when extending the codomain to real numbers, the $x$ would be mapped to an integer AND some different real number? – lightyourassonfire Jun 21 '23 at 23:24
  • Because once a single input has multiple outputs you no longer have a function. – ConMan Jun 21 '23 at 23:27
  • @lightyourassonfire: By definition, for every input, there is one and only one output. Anyway, if you include "codomain" as part of the definition of the function, then if you "extend the codomain" of a function, you are actually considering a different function. – Joe Jun 21 '23 at 23:28
  • Hello. Do you mind telling me what a relation from $A$ to $B$ in your book is defined to be? – Juliamisto Jun 21 '23 at 23:55
  • $\mathbb{Z}$ is countable while $\mathbb{R}$ is not, so there is no way a function can map each real to a unique integer. Such a function must be one-to-one, but the cardinalities don't allow that. – Chris Leary Jun 22 '23 at 00:29

2 Answers2

3

The notation $f:\mathbb{R}\to\mathbb{Z}$ means the domain of $f$ is $\mathbb{R}$ and the codomain of $f$ is $\mathbb{Z}$ but that does not mean the range of $f$ is all of $\mathbb{Z}$. For instance consider the function that maps any real number $x$ to $0$, i.e. the zero function $f(x)=0$ for all $x\in \mathbb{R}$. This function is not injective (does not map each input to a unique output).

Indeed that $\mathbb{Z}\subset \mathbb{R}$ implies that a larger codomain may be considered. In general, enlarging the codomain is not going to affect the range but may be done in various contexts where the "types" of points are important to consider. See @Jeppe Stig Nielsen's comment below.

Edit Let's clarify something about uniqueness. For a relation to be a function, it must not be multi-valued meaning we cannot have something like sending $a\to b$ and sending $a\to c$ and then happily consider this relation a function. This is what "unique" means in your book's function definition. But something like $a\to c$ and $b\to c$ is allowed. So, with your example, we have $f:A \to B$ by $1\to 8 \in B$ and we have $f:A\to C$ via $1\to 8\in B \subset C=\{8,9\}.$ Writing $f=\{(1,8), (1,9)\}$ is incorrect for the reasons stated at the onset of this edit--that (standard) functions cannot be multivalued.

Nap D. Lover
  • 1,292
  • 1
    If you have a function $f:\mathbb{R}\to\mathbb{Z}$, and you compare this to the function $g:\mathbb{R}\to\mathbb{R}$ that is obtained by enlarging the codomain (so for all $x$, we define $g(x)$ as the value $f(x)$), then it is mostly a matter of terminology if $f$ and $g$ are the "same" function or not (see answer by Akiva Weinberger). But in this situation, I think most would agree that the range of $f$ and the range of $g$ is the same. So what you are saying is some functions have range and codomain equal, and some do not. And my $g$ clearly does not. ($g$ is not surjective.) – Jeppe Stig Nielsen Jun 21 '23 at 23:30
  • @JeppeStigNielsen I agree, and I agree that your $f$ and $g$ have the same range. I wrote a little too fast and really meant to say that the range won't be equal to the new, larger codomain either. I'll make an edit. – Nap D. Lover Jun 21 '23 at 23:49
0

This depends on your definition of a "function". Some authors consider the codomain to be part of the information of a function; others don't. For the latter definition, every function $A\to B$ is also a function $A\to C$ if $B\subseteq C$.

Akiva Weinberger
  • 25,412
  • How do you define a function without specifying a codomain? In particular, I’m used to a function $f: A \to B$ being defined as a subset of $A \times B$ that obeys certain conditions. What definition can you use that does no codomain stuff? – Nicholas Priebe Jun 21 '23 at 23:54
  • @NicholasPriebe A subset of $A\times B$ is also a subset of $A\times C$, since $A\times B\subseteq A\times C$. – Akiva Weinberger Jun 22 '23 at 01:07