3

I need help to understand a question in combinatorics.

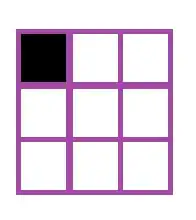
One corner square in a $3 \times 3$ grid is painted black, the other squares are white. In one move you can change color in all squares in a row or in a column. Can you get all the squares black after a number of such moves?

Hint: Study the number of black squares among the four corner squares

Does this regard a Rubiks cube? I cannot see other option that that, given the expression "in one move".

If not, any hints appreciated!

[[ Not looking for Solutions , only want Clarification on the Question ]]

Antonio De Angelis
  • 407
  • 3
  • 14
Superunknown
  • 3,089
  • Talking about Rubik's cubes, if you perform a permutation, like R, do those squares get black? – Antonio De Angelis Jun 21 '23 at 08:55
  • 1
    This is the definition of a "move". A "move" is changing the color of one row or one column. And then it is asking if you can achieve something by performing such moves. It could be called a "step" or "operation" instead of "move". It has nothing to do with any Rubik cube, it is about a square. – Michal Adamaszek Jun 21 '23 at 08:55
  • @MichalAdamaszek thanks, so if I change the colors of that row with the black square, it turns white and all the others in the row turn black. – Superunknown Jun 21 '23 at 08:59
  • 1
    Yes that would be right. – Michal Adamaszek Jun 21 '23 at 09:02
  • 1
    A reminder that this should be also tagged as contest-math –  Jun 21 '23 at 11:23

2 Answers2

2

It is a Planar Puzzle , not a Cubic Puzzle (Definitely not Rubic)

Putting in other words & Using Images may aid here , hence I will try that :

We have a 3×3 grid like given below  
One Corner Square in that is Initially painted Black.  
The other Squares are left White.  
Playing a game , you have 2 Possible moves :  
- you can change the colour in all Squares in a Selected row.  
- you can change the colour in all Squares in a Selected column.

Aim of the game is to make the grid all Black.

You can use these 2 moves in Succession.

Can you get all the Squares Black after a number of such moves ?

What is the Sequence of moves ?


Hint: Study the number of Black Squares among the four corner Squares

No Colouring :
3x3

Starting Position :
3x3

Playing with the move to the top row :
3x3

Ending Position :
3x3

Solution :

Not Posting the Puzzle Solution.  
OP wants Puzzle Explanation , not Puzzle Solution.

When OP responds , I may include that here.


My HINT : There is Some Invariant which we can try to Identify.

That Invariant will not change when making the moves.

That Invariant is not there in the Ending Position.
Prem
  • 14,696
  • Great illustration Prem. Thanks. I got a NO on this as answer. – Superunknown Jun 21 '23 at 09:05
  • 1
    Nice to know that it was useful , @Luthier415Hz , I was sure that you will not want the Solution & may want to think about it yourself ! – Prem Jun 21 '23 at 09:12
-5

Starting sequence:

[X][][]
[][][]
[][][]

...

Target sequence:

[X][X][X]
[X][X][X]
[X][X][X]

Solution:

I think it is unsolvable as the starting position is already in a non-solvable state. It represents a planar graph.

Prem's hint: Study the number of Black Squares among the four corner Squares

There is only 1 black square as a corner, it isn't solvable because of this principle.

Prem's hint 2: There is Some Invariant which we can try to Identify.

Prem's hint 3: That Invariant will not change when making the moves.

Prem's hint 4: That Invariant is not there in the Ending Position.

The upper left square is what is invariant, it will inevitably transform into a white square.

Antonio De Angelis
  • 407
  • 3
  • 14