Calculating volume of two perpendicular cylinders intersection

Question

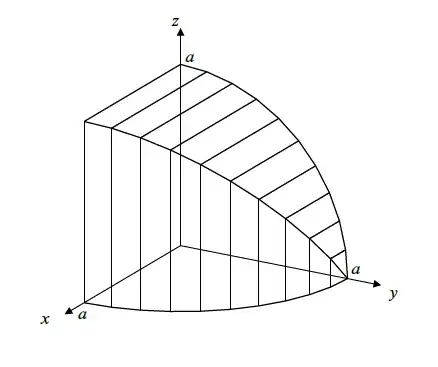
I want to calculate intersection of two cylinders: $x^2+y^2=a^2$, $y^2+z^2=a^2$ using triple integral.

$$8\int_0^a\int_0^\sqrt{a^2-x^2}\int_0^{\sqrt{a^2-y^2}}dz\,dy\,dx$$

I know answer of this problem is $\frac{16a^3}{3}$. But this integral is not solvable. Where am I wrong in writing intervals? I've read that upper bound for $z$ should be $\sqrt{a^2-x^2}$, but why? I think $z$ enters from $z=0$ and then exists in $z^2+y^2=a^2$, so I should be right. Where am I wrong?

This is similar to a recent hot question, also with $x^2+y^2=a^2$ on the $xy$-plane, and square slices perpendicular to an axis ($y$-axis in your case, $x$-axis in their case). — peterwhy, Jun 21 '23 at 01:04
To follow that recent hot question, if instead swap the outermost integral to $dy$, then the inner $\int_{0}^{\sqrt{a^2-y^2}}\int_{0}^{\sqrt{a^2-y^2}}dz\ dx$ becomes $\left(\sqrt{a^2-y^2}\right)^2$. — peterwhy, Jun 21 '23 at 01:14

score 0 · Answer 1 · answered Jun 23 '23 at 19:14

Steinmetz solid

However, the same problem had been solved earlier, by Archimedes in the ancient Greek world,[3][4] Zu Chongzhi in ancient China,[5] and Piero della Francesca in the early Italian Renaissance.[3] Read the Wikipedia article to follow the links.

Calculating volume of two perpendicular cylinders intersection

1 Answers1