Compute the integral: $\int_{0}^{\frac{\pi}{2}}\ln(\sec(x)+\tan(x))\csc(x)dx$

Question

This question is originally a simplified version from a qualifying exam problem from Archimedean Integration Bee (Cambridge University).

I tried doing angular symmetry but that gives me $$\int_{0}^{\frac{\pi}{2}}\ln(\csc(x)+\cot(x))\sec(x)dx.$$

I thought I could add both integrals and perform reverse product rule, but unfortunately $$\frac{d}{dx}\left [ \ln(\sec(x)+\tan(x))\ln(\csc(x)+\cot(x)) \right ]=\sec(x)\ln(\csc(x)+\cot(x))-\csc(x)\ln(\sec(x)+\tan(x)).$$ According to wolframalpha, the answer is $\frac{\pi^2}{4}$. This made me think that it uses some sort of Taylor Series somewhere, or a certain identity, but what's the quick solution to this problem?

Answer 1

Hint

If you use the tangent half-angle subsitution $$\int_0^{\frac \pi 2}\csc (x) \log (\tan (x)+\sec (x))\,dx=\int_0^{1}\frac 1 t \log \left(\frac{1+t}{1-t}\right)\,dt$$ Even the antiderivative is simple.

You could even simplify using $\frac{1+t}{1-t}=u$

Answer 2

Too long for a comment $$ I=\int_0^{\pi/2}\frac{\ln\frac{1+\sin x}{\cos x}}{\sin x}dx $$

$$ =-\int_0^{\pi/2}\frac{\ln\cos x}{\sin x}dx+\int_0^{\pi/2}\frac{\ln(1+\sin x)}{\sin x}dx $$

$$ =I_1+I_2 $$

Solving for $I_1$: $$ I_1\overset{t=\cos x}{=}-\int_0^1\frac{\ln t}{1-t^2}dt $$

$$ =-\frac12\int_0^1\frac{\ln t}{1-t}dt-\frac12\int_0^1\frac{\ln t}{1+t}dt$$ $$=-\frac12\int_0^1\frac{\ln (1-x)}{x}dx+\frac12\int_0^1\frac{\ln(1+ t)}{t}dt=\frac{\pi^2}8 $$

Solving for $I_2$ : $$ I_2=2\int_0^{\pi/4}\frac{\ln(1+2\sin t\cos t)}{2\sin t\cos t}dt\overset{x=\tan t}{=}-\int_0^1\frac{\ln(1+x^2)}{x}dx+\int_0^1\frac{\ln(1+x^2+2x)}xdx$$ $$=\frac32\int_0^1\frac{\ln(1+x)}xdx=\frac{\pi^2}8\,\, $$

$$ \Rightarrow\,\,I_1+I_2=\frac{\pi^2}4$$

Answer 3

Utilize $\int_0^{\pi/2}\frac{\cot y}{a^2\cot^2y+1}dy=\frac{\ln a}{a^2-1}$ with $a= \sec x+\tan x$

\begin{align} &\int_{0}^{\frac{\pi}{2}} \csc x\ln(\sec x+\tan x)\ dx\\ =&\int_{0}^{\frac\pi2} \int_{0}^{\frac\pi2} \frac{2\cot y \sec x(\sec x+\tan x)}{\cot^2y(\sec x+\tan x)^2+1}dy\ dx =\int_{0}^{\frac\pi2}2 y\ dy=\frac{\pi^2}4 \end{align}

Answer 4

Splitting the integral into two, we have $$ \int_0^{\frac{\pi}{2}} \frac{\ln (\sec x+\tan x)}{\sin x} d x = \underbrace{\int_0^{\frac{\pi}{2}}\frac{\ln (1+\sin x)}{\sin x}dx}_{J} - \underbrace{\int_0^{\frac{\pi}{2}}\frac{\ln \cos x}{\sin x}d x}_{K} $$ For $J$, considering $I(\theta)=\int_0^{\frac{\pi}{2}} \frac{\ln (1+\cos \theta \sin x)}{\sin x} d x$ and differentiating $I(\theta)$ w.r.t. $\theta$ gives $$ I^{\prime}(\theta)=\int_0^{\frac{\pi}{2}} \frac{-\sin \theta}{1+\cos \theta \sin x} d x=-\sin \theta\left(\frac{\theta}{\sin \theta}\right)=-\theta, $$ where the second last step comes from the result of the post.

Therefore $$ \begin{aligned} & I(0)-I\left(\frac{\pi}{2}\right)=\int_{\frac{\pi}{2}}^0-\theta d \theta \\ \Leftrightarrow \quad &\int_0^{\frac{\pi}{2}} \frac{\ln (1+\sin x)}{\sin x}=-\left[\frac{\theta^2}{2}\right]_{\frac{\pi}{2}}^0=\frac{\pi^2}{8} \end{aligned} $$ For $K$, letting $y=\cos x$ yields $$ K=\int_0^1 \frac{\ln y}{1-y^2} d y=-\frac{\pi^2}{8} $$ Combining $J$ and $K$ yields $$\boxed{\int_0^{\frac{\pi}{2}} \frac{\ln (\sec x+\tan x)}{\sin x} d x = J-K=\frac{\pi^2}{4}}$$

Answer 5

As @Claude Leibovici’s suggested,

$$\int_0^{\frac \pi 2}\csc (x) \ln (\tan (x)+\sec (x))\,dx \stackrel{t=\tan \frac{x}{2}}{=} \int_0^{1}\frac 1 t \ln\left(\frac{1+t}{1-t}\right)\,dt$$ For the last integral, we use the substitution $u=\frac{1-t}{1+t}$, then \begin{aligned} I & =\int_1^0 \frac{1+u}{1-u} \ln \frac{1}{u} \cdot\left(-\frac{2}{(1+u)^2} d u\right) \\ & =-2\int_0^1 \frac{\ln u}{1-u^2} d u \\ & =\frac{\pi^2}{4} \end{aligned}

Answer 6

Here's an approach that yields the indefinite integral, too: Applying the tangent half-angle substitution, $$x = 2 \arctan t, \qquad dx = \frac{2 \,dt}{1 + t^2},$$ transforms the integral to $$\require{cancel}\int_0^1 \left(\frac{\log (1 + t)}{t} - \frac{\log(1 - t)}{t} \right) dt = \left.\operatorname{Li}_2(t) - \operatorname{Li}_2(-t) \right\vert_0^1 = \frac{\pi^2}{6} - \left(-\frac{\pi^2}{12}\right) = \frac{\pi^2}{4},$$ where $\operatorname{Li}_2$ is the dilogarithm.

Alternatively, one can interpret $\int_0^1 \frac{\log (1 \pm t)}{t} \,du$ as the series $\sum_{k = 1}^\infty \frac{(\mp 1)^k}{k^2}$ and apply the well-known identity $\sum_{k = 1}^\infty \frac{1}{k^2} = \frac{\pi^2}{6} .$

Answer 7

Expanding on @Lai's answer: Using the tangent half-angle substitution, $t=\tan(x/2)$, we get $$\cos x=\frac{1-t^2}{1+t^2},\qquad\sin x=\frac{2t}{1+t^2},\qquad dx=\frac{2dt}{1+t^2},$$ so that $$J=\int_0^{\pi/2}\log\left(\frac{1}{\cos x}+\frac{\sin x}{\cos x}\right)\frac{dx}{\sin x}\\ =\int_0^1\log\left(\frac{1+t^2}{1-t^2}+\frac{\tfrac{2t}{1+t^2}}{\tfrac{1-t^2}{1+t^2}}\right)\frac{1+t^2}{2t}\frac{2dt}{1+t^2}\\= \int_0^1\log\left(\frac{1+t}{1-t}\right)\frac{dt}{t}.$$ Then integration by parts gives $$J=-2\int_0^1\frac{\log t}{1-t^2}dt=-2\sum_{n\ge0}\int_0^1 t^{2n}\log(t)dt.$$ Noticing that $$I(a)=\int_0^1x^adx=\frac{1}{a+1}\Rightarrow I'(a)=\int_0^1x^a\log(x)dx=-\frac{1}{(a+1)^2},$$ we have $$J=2\sum_{n\ge0}\frac{1}{(2n+1)^2}=2\left(\sum_{n\ge1}\frac{1}{n^2}-\sum_{n\ge1}\frac{1}{(2n)^2}\right)=2\left(\frac{\pi^2}{6}-\frac{\pi^2}{24}\right)=\frac{\pi^2}{4}.$$

Answer 8

Use the Gudermannian Function by $$ x = 2\arctan\left(e^u\right) - \frac{\pi}{2} = \operatorname{gd}(u). $$ Then $$ \begin{align} I &:= \int_{0}^{\frac{\pi}{2}}\ln\left(\sec x+\tan x\right)\csc xdx \\ &= \int_{0}^{\infty}\ln\left(\sec\left(\operatorname{gd}(u)\right)+\tan\left(\operatorname{gd}(u)\right)\right)\csc\left(\operatorname{gd}(u)\right)\cdot\frac{d}{du}\left(\operatorname{gd}(u)\right)du \\ &= 2\int_{0}^{\infty}\frac{ue^{-u}}{1-e^{-2u}}du \\ &= 2\sum_{n=0}^{\infty}\int_{0}^{\infty}ue^{\left(1-2n\right)u}du \\ &= \sum_{n=0}^{\infty}\frac{2}{\left(2n+1\right)^{2}} \\ &= \frac{\pi^{2}}{4}. \\ \end{align} $$

---

Here is an alternate (and non-integration-bee-friendly) solution. Map $x \mapsto 2\arctan x$. Then

$$ I := \int_{0}^{1}\ln\left(\sec\left(2\arctan x\right)+\tan\left(2\arctan x\right)\right)\csc\left(2\arctan x\right)\left(\frac{d}{dx}2\arctan x\right)dx \\ $$ which simplifies down to

$$ \begin{align} I &= \int_{0}^{1}\frac{1}{x}\ln\left(\frac{1+x}{1-x}\right)dx \\ &= \int_{0}^{1}\frac{\ln\left(1+x\right)}{x}dx-\int_{0}^{1}\frac{\ln\left(1-x\right)}{x}dx \\ &= \int_{0}^{-1}\frac{\ln\left(1-x\right)}{x}dx-\int_{0}^{1}\frac{\ln\left(1-x\right)}{x}dx \\ &= -\int_{-1}^{1}\frac{\ln\left(1-x\right)}{x}dx. \\ \end{align} $$

Let $f(z) = \displaystyle \frac{\log (1-z)}{z}$ where $\arg(1-z) \in (-\pi,\pi]$ so that the branch cut is on $[1,\infty)$. The function has a removable singularity at $z=0$ because $\displaystyle f(z) = -1-\frac{z}{2}-\frac{z^{2}}{3}-\frac{z^{3}}{4}+O\left(z^{6}\right)$, and so $f(z)$ doesn't blow up as $z \to 0$. Choose any small radius $r \ll 1$. We travel counterclockwise around $C$, which we define as the union of the three sets $C_1 = [-1,1-r]$, $\displaystyle C_{2}=\left[1-r,1-\frac{r^{2}}{2}+\frac{ir}{2}\sqrt{4-r^{2}}\right]$, and $\displaystyle C_{3}=\left[1-\frac{r^{2}}{2}+\frac{ir}{2}\sqrt{4-r^{2}},-1\right]$. Here, $C_2$ is the small arc and $C_3$ is the big arc illustrated below.

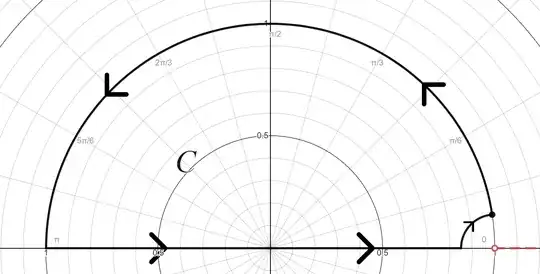
Cauchy's Integral Theorem allows us to write $\displaystyle \oint_{C} f(z)dz$ as

$$ 0 = \int_{C_1}f(z)dz + \int_{C_2}f(z)dz + \int_{C_3}f(z)dz. $$

By equating $\Re$ and making $r \to 0^+$ on both sides, we get

$$ I = \Re \lim_{r \to 0^+} \int_{C_2}f(z)dz + \Re \lim_{r \to 0^+} \int_{C_3}f(z)dz. $$

For the small arc, parameterize $z = 1-re^{-i\theta}$ where $\displaystyle \theta \in \left[0, \arcsin{\left(\frac{1}{2}\sqrt{4-r^2}\right)}\right]$. Then we use the ML-inequality $$ \left|\int_{C_2}f(z)dz\right| \leq ML. $$ We find $L$ by the arc length formula for a circle like $$ L = r \arcsin{\left(\frac{1}{2}\sqrt{4-r^2}\right)}. $$ We find $M$ by bounding $|f(z)|$ like $$ \left|\frac{\log\left(1-z\right)}{z}\right|\le\frac{\left|\ln\left|1-z\right|\right|+\left|i\arg\left(1-z\right)\right|}{\left|z\right|}\le\frac{\left|\ln\left|1-\left(1-re^{-i\theta}\right)\right|\right|+\pi}{\left|1-re^{-i\theta}\right|}\le\frac{\pi-\ln r}{1-r}. $$

The Squeeze Theorem should make things easier from here. The integral over $C_2$ goes to $0$ as $r \to 0^+$.

For the other integral, parameterize $z = e^{it}$ where $\displaystyle t \in \left[\arccos{\left(1-\frac{r^2}{2}\right)}, \pi\right]$. Then

$$ \begin{align} \Re \lim_{r \to 0^+} \int_{C_2}f(z)dz &= \Re \lim_{r \to 0^+}\int_{\arccos\left(1-\frac{r^{2}}{2}\right)}^{\pi}\frac{\log\left(1-e^{it}\right)}{e^{it}}\cdot ie^{it}dt \\ &= \Re\int_{0}^{\pi}\left(i\ln\left|1-e^{it}\right|-\arg\left(1-e^{it}\right)\right)dt \\ &= \Re i\int_{0}^{\pi}\ln\left|1-e^{it}\right|-\Re\int_{0}^{\pi}\arctan\left(\frac{-\sin t}{1-\cos t}\right)dt \\ &= 0+\int_{0}^{\pi}\arctan\left(\tan\left(\frac{\pi}{2}-\frac{t}{2}\right)\right)dt \\ &= \frac{\pi^{2}}{4}. \\ \end{align} $$

Therefore,

$$ I = 0 + \frac{\pi^2}{4} = \frac{\pi^2}{4} $$

and we're done!