The definition of the derivative of $f$. Matrix vs. Linear Mapping.

Question

The following definitions are two definitions of the derivative of $f$.

Definition. (Definition 1) Let $A\subset\mathbb{R}^m$, let $f:A\to\mathbb{R}^n$. Suppose $A$ contains a neighborhood of $a$. We say that $f$ is differentiable at $a$ if there is an $n$ by $m$ matrix $B$ such that $$\frac{f(a+h)-f(a)-B\cdot h}{|h|}\to 0\,\,\,\,\,\,\text{as}\,\,\,\,\,\,h\to0.$$ The matrix $B$, which is unique, is called the derivative of $f$ at $a$; it is denoted $Df(a)$.

Another Definition. (Definition 2) Let $A\subset\mathbb{R}^m$, let $f:A\to\mathbb{R}^n$. Suppose $A$ contains a neighborhood of $a$. We say that $f$ is differentiable at $a$ if there is a linear mapping $B$ such that $$\frac{f(a+h)-f(a)-B(h)}{|h|}\to 0\,\,\,\,\,\,\text{as}\,\,\,\,\,\,h\to0.$$ The linear mapping $B$, which is unique, is called the derivative of $f$ at $a$; it is denoted $Df(a)$.

---

Suppose we must solve the following problem.

Let $f:\mathbb{R}^2\to\mathbb{R}^2$ be a function such that $f(\begin{pmatrix}x\\y\end{pmatrix})=\begin{pmatrix}e^x\sin y\\x^2 e^y\end{pmatrix}$.
Let $c:=\begin{pmatrix}a\\b\end{pmatrix}$.
Find $Df(c)$.

If we adopt the Definition 1, our answer is like the following:

$Df(c)=\begin{pmatrix}e^a\sin b&e^a \cos b\\2a e^b&a^2 e^b\end{pmatrix}.$

If we adopt the Definition 2, our answer is like the following:

$Df(c)$ is the lienar mapping such that $\mathbb{R}^2\ni \begin{pmatrix}x\\y\end{pmatrix}\to\begin{pmatrix}e^a\sin b&e^a \cos b\\2a e^b&a^2 e^b\end{pmatrix}\begin{pmatrix}x\\y\end{pmatrix}\in\mathbb{R}^2.$

---

I think Definition 1 is better than Definition 2.
But some authors adopt Definition 2.
I want to know an advantage of Definition 2.

---

peek-a-boo, Thank you very much for your kind answer.

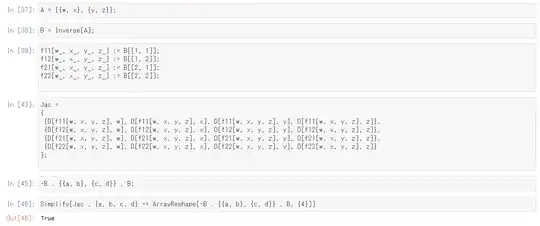
Let $f:GL(2,\mathbb{R})\ni A\to A^{-1}\in GL(2,\mathbb{R})$.
I checked $Df_A(\xi)=-A^{-1}\xi A^{-1}$ holds when $n=2$ by Wolfram Engine. (Please see the answer by peek-a-boo.)

Answer 1

Definition 2 using linear transformations is better. This applies more generally even when your vector spaces are not $\Bbb{R}^n,\Bbb{R}^m$. It holds for arbitrary finite-dimensional and even infinite-dimensional vector spaces.

Matrices are a pain conceptually. And computationally, they’re a mess to deal with if you’re not dealing with $\Bbb{R}^n,\Bbb{R}^m$. If for example you modify your domain to a finite-dimensional space of matrices, even something as innocuous as $M_{a\times b}(\Bbb{R})$, and your target to $\Bbb{R}^n$ or something else, then trying to work with the derivative as a matrix is a mess, because you must first choose a basis for the domain and target, and this is not canonical. If you don’t believe me, then look online for the dozens of “matrix calculus” formulae, or just search on this site for the hundreds of matrix-calculus based questions where people are confused by rows vs columns and other silly matters. So many different conventions for the ordering, layouts, transpose issues etc etc. It’s all a mess. Of course, to code it into a computer, you have no other choice, but conceptually, and even for many practical hands-on calculations, it’s a nightmare; it’s only decent if you’re restricting yourself to first derivatives, and maps $f:\Bbb{R}^n\to\Bbb{R}^m$. If you want to go beyond first derivatives, or these specific domains and targets, the matrix approach quickly becomes intractable.

Linear transformations, by their very definition are more general, so more widely applicable. Also, it emphasizes the fundamental idea of differential calculus: local approximation by linear functions. Higher derivatives become easier to handle conceptually (they’re multilinear maps, and by Schwarz’s theorem, they’re symmetric). Taylor’s theorem becomes easy to state, and it’s almost identical to the single-variable case (see here and the links within). And surely, you’d agree Taylor’s theorem was important in one-dimension, so understanding it in higher dimensions is all the more important.

---

Here’s a concrete example. Consider the inversion map $f:GL(n,\Bbb{F})\to GL(n,\Bbb{F})$, $f(A)=A^{-1}$ where $\Bbb{F}$ is either $\Bbb{R}$ or $\Bbb{C}$. This is a differentiable map (actually it is analytic), and its derivative at a point $A\in GL(n,\Bbb{F})$ evaluated on $\xi\in M_{n\times n}(\Bbb{F})$ is \begin{align} Df_A(\xi)&=-A^{-1}\xi A^{-1}. \end{align} (In the case $n=1$, this is like saying $\frac{1}{x}$ has derivative $-\frac{1}{x^2}$, but this way of writing takes the non-commutativity of matrices into account). Or, if we use differential-forms notation, then \begin{align} d(A^{-1})&=-A^{-1}\cdot dA\cdot A^{-1}. \end{align} You see, things are very easily expressible and you can understand what’s going on. Trying to write the linear transformation $Df_A$ as a matrix requires an $n^2\times n^2$ matrix, which is a complete hassle, and completely obscures what’s going on.

Next, an infinite-dimensional example: a whole chunk of calculus of variations can be dealt with using the Frechet derivative, in the context of say the Banach space $C^1([a,b])$. In infinite-dimensions, there are no matrices. Anyway, I don’t want to use infinite-dimensionality as a motivation for the linear-transformation approach; even in finite dimensions, the fact that a matrix-representation requires a choice of basis already makes it highly inconvenient.