My ideas aren't completely thought-through, but here's what I've come up with so far:
$\Large \text{Switching colors}$
The idea here is to "pair up" games to prove that the total number of games is even.
Given a position for the white pieces, we'll try to construct the exact same position, but for the black pieces. This can be accomplished by making white "skip" a turn toward the start of the game, making it look like black had made the first move. Doing this is simple, though it requires that some of your pieces have space to move.
Here's an example of how it can be done, the idea being that white spends 3 turns moving a piece away and back to its original position while black only takes 2 turns:
e4 - e5 - Bd3 - Be7 - Be2 - Bf8 - Bf1
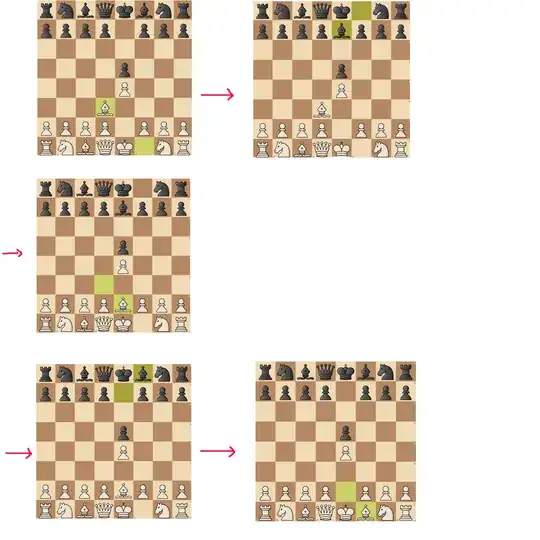
Performing a such a sequence requires that both sides have a rook, bishop or queen with enough space to move away and back. I believe that any game that doesn't end in an early stalemate due to horses moving around presents a such opportunity.
The game isn't completely identical when black "starts", but its basically just normal chess flipped horizontally and vertically, so I'd expect the set of playable games in either version to be the same.
Note that this can't be done with knights since they always take an even number of turns to return to a square.
There's another approach that one can consider:
$\Large \text{Permutating knights}$
As was mentioned by @DanUznanski in a comment, you can create copies of any given game by moving knights around before the first $real$ move.
Any given permutation of knights can be mirrored on the $y-$axis. Consequently, given $n$ permutations starting with $Nf3$, there are $n$ corresponding permutations starting with $Nc3$ (all later moves are also mirrored), making for a total even number of $2n$ permutations.
That means that, given any game, there are $2n$ ways to append knight permutations to the start, giving you $2n$ "copies" of said game.
Also counting the game that doesn't have any prepended permutations, there are a total of $2n + 1$ "versions" of each game. Since $2n + 1$ is odd, this approach currently doesn't deliver meaningful evidence.
There is, however, something I skipped, that may change the result: permutations where a white knight lands on $c6$ or $e6$ can't be mirrored, because, landing on $d6$ or $f6$, they'd put the black king in check, forcing him to move or take the knight (and thus invalidating the permutation). The same problem can occur for black knights. This means that certain permutations don't have a corresponding mirrored equivalent. I believe that the number of thus lost possibilities is even, meaning that the total number of $versions$ of a given match would still be odd.
Deeper analysis may, however, reveal that the number of lost possibilities is odd, which would render this method fruitful, proving that the total number of games is even.
P.S. could anyone be so kind as to embed the image? I don't have enough reputation to.
$\Large \text{Response to Prem's answer}$
First off, thank you for your feedback to my ideas.
I don't quite understand what you mean with (1), so I'll address the other ones for now:
(2) I do believe that a match-up is nonetheless always available, since, apart from left and right having been switched, everything is still the same (relative position of pieces, long castle towards queen, etc.)
(3 - 6) I see what you mean, and it may indeed pose a problem.
My idea was that the match-up is made as early on in the game as possible, avoiding the problems that you mentioned.
This would, of course, require checking that a color-swap can always be achieved before checkmate, similarly to how you would check the parity of starting positions. I do believe that it'll always be possible, since it only requires pawns moving to make sufficient space for a bishop, queen, ... to perform the color switch.

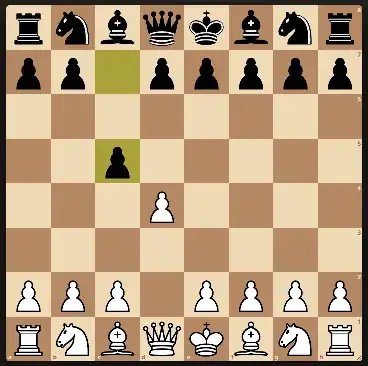
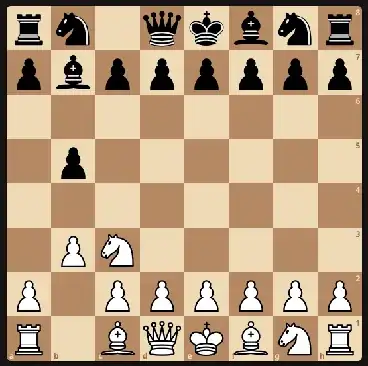
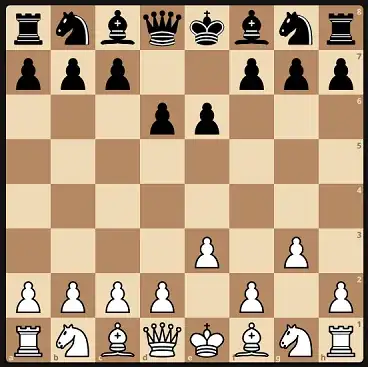
A more refined parity argument, showing that, for each position reachable only through knight moves, there are an even number of ways to reach it, would do the trick, since, once a pawn moves, we will never reach a previous position again
– Gavin Dooley Jul 22 '24 at 13:13