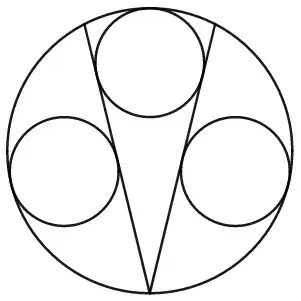
Inspired by this Sangaku-style question about a constellation of circles, I've come up with the following question.
How can we construct, with straightedge and compass, the following diagram?
Description: In a (large) circle, two equal length chords share a point on the circle. In each of the two segments thus formed, a largest possible circle is inscribed. A third circle touches the large circle and both chords. The three inscribed circles are of equall radii.
The ratio of the large circle's radii to the smaller circles' radii is $\phi+1$, where $\phi=\frac{1+\sqrt5}{2}$ is the golden ratio (proof).
If we construct the chords, then the circles are easy to draw. But how can we construct the chords?