University of Cambridge: Mistake on the exam? Extending holomorphic functions on intersecting discs

Question

Consider the following question

Let $D_1$ and $D_2$ be two overlapping closed discs. Let $f$ be a holomorphic function on some open neighborhood of $D = D_1 \cap D_2$. Show that there exist open neighborhoods $U_j$ of $D_j$ and holomorphic functions $f_j$ on $U_j$ for $j = 1, 2$, such that $f(z) = f_1(z) + f_2(z)$ on $U_1 \cap U_2$.

I am convinced that this is not necessarily true. Here is my counter-example:

Let $D_1$ and $D_2$ be the red and blue circles in the bellow diagram. Morever, let the black one be the unit disc. 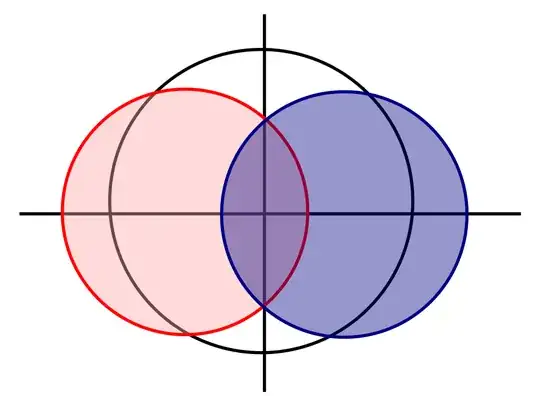Let $$ f(z) = \sum_{n=1}^\infty z^{2^n}. $$ Per this question, the function does not have an analytic continuation that contains any part of the unit circle. Now, in the question, by the identity theorem, we must have $$ f_1 = f_2 = \frac{1}{2}f $$ on $D$. As $f_1$ is holomorphic on $U_1$, it is holomorphic on $D_1$. But this together with the identity theorem on $D_1 \cap D$ gives us that $f$ can be analytically extended through the unit circle, which can not be true.

Question: Is my counter example correct?

Answer 1

Let $U$ be the neigbourhood of $D$ on which $f$ is defined, let $\Delta$ be a neighbourhood of $D$ contained in $U$ and let $C$ be the boundary of $\Delta$. Then, in $\Delta$, $$f(z)=\frac{1}{2\pi i}\int_{C}\frac{f(\lambda)}{\lambda-z}d\lambda.$$ Split the boundary into two continuous parts $C_1$ and $C_2$ so that their union is $C$ and $C_1 \cap D_1 = \emptyset$, $C_2 \cap D_2 = \emptyset$ (it is 'obvious' from a picture that you can do this, but you would need to prove it). Then you can use the first result in the question to define $f_1$ as $$f_1(z)=\frac{1}{2\pi i}\int_{C_1}\frac{f(\lambda)}{\lambda-z}d\lambda,$$ which will be holomorphic on $D_1$ and $f_2$ as $$f_2(z)=\frac{1}{2\pi i}\int_{C_2}\frac{f(\lambda)}{\lambda-z}d\lambda,$$ which will be holomorphic on $D_2$. The sum of $f_1$ and $f_2$ will equal $f$ in $\Delta$.

Answer 2

The statement in the question is correct, and your example it not a counterexample.

$f_1$ is defined and holomorphic in a neighborhood $U_1$ of $D_1$, $f_2$ is defined and holomorphic in a neighborhood $U_2$ of $D_2$, and $f_(z) = f_1(z) + f_2(z)$ holds for all $z \in U_1 \cap U_2$. It does not follow that $f_1 = f_2$ in $ U_1 \cap U_2$, or that $f$ can be continued analytically beyond any point of its domain.

Here is a simpler example: The function $$ f : \Bbb D \to \Bbb C, f(z) = \frac{1}{1-z^2} $$ is holomorphic in the unit disk and has singular points at $z=-1$ and $z=1$. If we define $$ f_1 : B(-1, \sqrt 2) \to \Bbb C, f(z) = \frac{1}{2(1-z)} \, ,\\ f_2 : B(1, \sqrt 2) \to \Bbb C, f(z) = \frac{1}{2(1+z)} $$ then $f_1$ and $f_2$ are holomorphic in the disks $D_1 = B(-1, \sqrt 2)$ and $D_2 = B(1, \sqrt 2)$, respectively.

For $z \in D_1 \cap D_2$ is $$ f_1(z) + f_2(z) = \frac{1}{2(1-z)}+\frac{1}{2(1+z)} = \frac{1}{1-z^2} = f(z) $$ so we have a decomposition as in the given question. But it does not follow that $f_1 = f_2 = \frac{1}{2}f$ in $D_1 \cap D_2$, or that $f$ can be continued analytically beyound its singular points $z=1$ or $z=-1$.