Proving that $S(x_0,r) \subseteq \overline{B(x_0,r)}$

Question

I 'm trying to prove the statement above, that "$S(x_0,r) \subseteq \overline{B(x_0,r)}$ $\forall x\in X$ and every $r>0$, where $(X,\rho)$ is a metric space with $\rho$ being a norm", as a part of an exercise that has got me to this point. I 've consulted the solutions manual, and the proof that it gives for the statement uses the sequential characterization of closedness of the set and of contact points to get to the result. I understand the proof, however, based on the level I 'm at right now, I believe that I would not be able to come up with the sequence the instructor defines by myself, so I tried to go straight with the proof, without any fancy tricks;

I want to prove that, for a given $x\in X$ and $r>0$, $S(x_0,r) \subseteq \overline{B(x_0,r)}$. So if $y\in S(x_0,r)$, I want to show that $y\in \overline{B(x_0,r)}$.

Now, by the definition of the closure of a set, $y\in \overline{A} \implies \forall \varepsilon>0, B(y,\varepsilon)\cap A \neq \emptyset$.

So I want to show that if $y\in S(x_0,r)$, then $\forall \varepsilon>0, B(y,\varepsilon)\cap B(x_0,r) \neq \emptyset$. In other words, $\exists z\in B(y,\varepsilon) : z\in B(x_0,r)$ Finally, this translates to

$\forall \varepsilon>0, \exists z\in X : \rho(z,y)<\varepsilon$ and $\rho(z,x_0)<r$

I 'm trying to prove this by contradiction. This would translate to:

"Suppose that $\exists \varepsilon>0$, so that $\forall z\in X$, if $\rho(z,y)<\varepsilon$, then $\rho(x_0,z)\geq r$" (*)

(Remember that $y\in S(x_0,r)$, so $\rho(y,x_0)=r$).

And this is where I have got to. What I was trying to achieve, is (through the property of the trigonometric inequality) to get to something like $\rho + \varepsilon < \rho$, but no matter what manipulations I do, I can't seem to see the light. Maybe this is because, the (*) is indeed true for some $z\in B(y,\varepsilon)$, but certainly not for all. The only thing I can think of, is that I have not used the fact that $\rho$ is a norm, but I don't see the way this would add something to the solution. What strikes me the most is that geometrically, the statement is geometrically fairly easy to see that is true: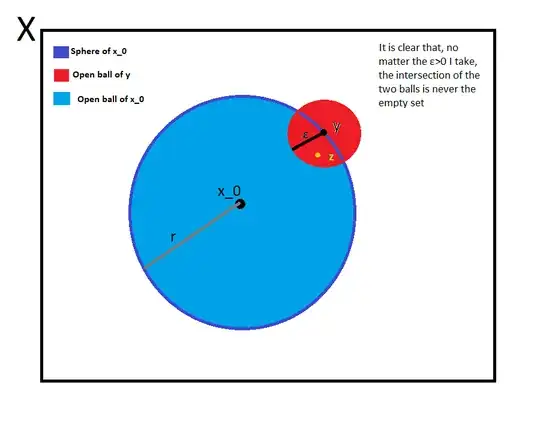

That's it, I 'm really sorry for the long text. Any help would be greatly appreciated!

Maybe im missing something but $\overline{B(x_0, r) }=B(x_0, r) \cup S(x_0, r) $ — Guillermo García Sáez, May 27 '23 at 18:38
@GuillermoGarcíaSáez Sure, but they haven't proven that yet. — FShrike, May 27 '23 at 18:39
To the OP: if you are worried about using the sequential characterisation of closure, you should tell us what definition of "closure" you are using. In metric spaces, there are a few you could use — FShrike, May 27 '23 at 18:40
@FShrike I 'm using the standard definition, $y\in \overline{A} \implies \forall \varepsilon>0, B(y,\varepsilon)\cap A \neq \emptyset$. The solution manual defines the sequence $y_{n}=x+t_{n}(x-y)$, where $t_{n}$ a sequence in $(0,1)$ with $t_{n}\to 1$. Maybe, after I solve 50, or 100 exercises, I will be able to use tricks like this, but for the moment, there is no way I would be able to come up with this on my own. So I tried to solve the problem using the standard definitions and the geometric intuition of things. Maybe I 'm a bit stubborn, but I see no reason why it wouldn't be possible. — User0207, May 27 '23 at 19:08
@chris12345 "The standard definition" of closed is "the complement is open". It's common for questions to be asked here about metric spaces where the OP is using one definition and everyone helping them is using another... so I just wanted to avoid that — FShrike, May 27 '23 at 19:13
I also notice that there is crucial context of there being some kind of linear structure to your space (you can add elements) and the result isn't necessarily true without that structure. — FShrike, May 27 '23 at 19:20
I don't think the statement is true unless X is a linear normed space. For example, suppose $X={x\in\mathbb{R}: |x|\leq1/2}\cup{1,-1}$ with the metric inherited from the norm in $\mathbb{R}$. $B(0;1)={x\in X:|x|<1}={x\in\mathbb{R}: |x|\leq1/2}$ is a closed subset of $X$ and $S(0;1)={x\in X:|x|=1}={-1,1}$ is not contained in the closure of $B(0,1)$ in $X$. — Mittens, May 27 '23 at 20:59
Does this answer your question? When is the closure of an open ball equal to the closed ball? — Mittens, May 27 '23 at 21:53
Alright guys, n.1 both of you are correct, the statement isn't always true in any metric space, and in fact I was asked to prove this in another exercise. Obviously taking $\rho$ being a norm changes the nature of the space, opposing to it being a distance funstion. Seems I'm missing sth regarding the properties of norms, so maybe I'll need to look up some things before I give this proof another shot. In any way, I thank you both! @OliverDíaz — User0207, May 28 '23 at 09:08

score 1 · Answer 1 · answered May 27 '23 at 19:20

If $S(x_0,r)$ is empty, we are done. I'm assuming $X$ is a normed linear space and that $r>0$.

Suppose $y\in S(x_0,r)$, and fix $\epsilon>0$. Without loss of generality, suppose that $\epsilon<2r$ as well.

The element $y':=y-\frac{1}{2r}\epsilon(y-x_0)$ satisfies $\rho(y',y)<\epsilon$ and $\rho(x_0,y')=r|1-\epsilon/2r|=r-\epsilon/2<r$. Therefore $y'$ witnesses the fact that $B(x_0,r)\cap B(y,\epsilon)\neq0$. Since $\epsilon$ and $y$ are both taken arbitrarily, it follows that $S(x_0,r)\subseteq\overline{B(x_0,r)}$.

The geometric intuition? You're at the boundary of the ball, and you're just moving a tiny distance inwards along the line from the boundary point to the centre. That tiny distance by which you have moved is enough to bring you inside $B(x_0,r)$ without moving too far away from the boundary.

In general for general metric spaces this is false. Consider the discrete metric space on a set with at least two distinct elements, $a$ and $b$. $B(a,1)=\{a\}$ and $b\in S(a,1)$ however $b\notin\overline{B(a,1)}=B(a,1)=\{a\}$.

Proving that $S(x_0,r) \subseteq \overline{B(x_0,r)}$

1 Answers1