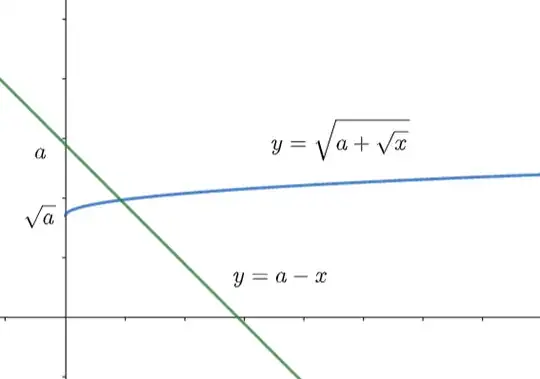
Reading the answers, I first thought that some answers show an incorrect proof for the claim that the equation has a solution if and only if $a\ge 1$.
However, "incorrect" is perhaps too strong a word.
I'm going to write a solution first, and then show some thoughts about a solution, and finally write another solution which tries to avoid using "squaring".
A solution :
From
$$x+\sqrt{a+\sqrt x}=a\tag1$$
we have to have
$$x\ge 0\qquad\text{and}\qquad a\gt 0\tag2$$
($a\gt 0$ because LHS $\ge 0$, and $a$ is non-zero).
Under $(2)$, we have (as some other answers did)
$$\begin{align}(1)&\iff \sqrt{a+\sqrt x}=a-x
\\\\&\iff a+\sqrt x=(a-x)^2\qquad\text{and}\qquad a-x\gt 0
\\\\&\iff a^2+(-2x-1)a+x^2-\sqrt x=0\qquad\text{and}\qquad a-x\gt 0
\\\\&\iff a=\frac{2x+1\pm\sqrt{4x+4\sqrt x+1}}{2}\qquad\text{and}\qquad a-x\gt 0
\\\\&\iff a=\frac{2x+1\pm\sqrt{(2\sqrt x+1)^2}}{2}\qquad\text{and}\qquad a-x\gt 0
\\\\&\iff a=\frac{2x+1\pm (2\sqrt x+1)}{2}\qquad\text{and}\qquad a-x\gt 0
\\\\&\iff a=x+\sqrt x+1,x-\sqrt x\qquad\text{and}\qquad a-x\gt 0
\\\\&\iff a=x+\sqrt x+1\tag3\end{align}$$
Now, let us prove that $(1)$ has a solution if and only if $a\ge 1$.
Since we've already seen that $(1)$ has a solution if and only if $(3)$ has a solution, it is sufficient to prove that $(3)$ has a solution if and only if $a\ge 1$.
If $(3)$ has a solution, then $a=x+\sqrt x+1\ge 1$.
If $a\ge 1$, then $$\begin{align}(3)&\iff \bigg(\sqrt x+\frac 12\bigg)^2=a-1+\frac 14\\\\&\iff \underbrace{\sqrt x+\frac 12}_{\color{red}{\text{positive}}}=\color{red}+\sqrt{\underbrace{a-1}_{\ge\ 0}+\frac 14}\ \ \bigg(\ge\sqrt{\frac 14}=\frac 12\bigg)\end{align}$$ so $(3)$ has a solution.
It follows that $(3)$ has a solution if and only if $a\ge 1$.
Therefore, we can say that $(1)$ has a solution if and only if $a\ge 1$.
Since we get $\sqrt x=\sqrt{a-\frac 34}-\frac 12$, we finally obtain
$$x=\bigg(\sqrt{a-\frac 34}-\frac 12\bigg)^2=\frac{2a-1-\sqrt{4a-3}}{2}$$
Next, I'm going to show some thoughts about the following solution.
"We have $x+\sqrt x+1=a$. Solving this, we get $\sqrt x=\frac{-1\pm\sqrt{4a-3}}{2}$. Since we can exclude $\frac{-1-\sqrt{4a-3}}{2}$, we get $\sqrt x=\frac{-1+\sqrt{4a-3}}{2}$. A necessary and sufficient condition for this to be real and non-negative is $4a-3\ge 0$ and $\frac{-1+\sqrt{4a-3}}{2}\ge 0$, i.e. $a\ge 1$."
I first thought that this solution is incorrect. The reason is as follows :
$\sqrt x=\frac{-1+\sqrt{4a-3}}{2}$ is valid only when $a\ge 1$ (since LHS is real and non-negative). So, when one writes $\sqrt x=\frac{-1+\sqrt{4a-3}}{2}$, one implicitly assume $a\ge 1$ (If $a\lt 1$, then $\sqrt x=\frac{-1+\sqrt{4a-3}}{2}$ does not make sense).
Then, I received the following comment :
It looks to me that you are ignoring the fact that quadratic equation always has two complex solutions. One can observe a posteriori that out of these two solutions, there is a real nonnegative solution if and only if $a≥1$.
It seems that this comment suggests the following :
"We have $x+\sqrt x+1=a$. There are two complex solutions $\sqrt x=\frac{-1\pm\sqrt{4a-3}}{2}$. Since we can exclude $\frac{-1-\sqrt{4a-3}}{2}$, we get $\sqrt x=\frac{-1+\sqrt{4a-3}}{2}$. A necessary and sufficient condition for this to be real and non-negative is $4a-3\ge 0$ and $\frac{-1+\sqrt{4a-3}}{2}\ge 0$, i.e. $a\ge 1$."
This makes sense, so "incorrect" is perhaps too strong a word.
Some comments :
Since the "solution" in "the equation has a solution if and only if $a\ge 1$" is real, I thought that we have to solve our problem only in real numbers.
There is a short solution only in real numbers. For example, see the above solution of mine. So, our problem can be solved only in real numbers.
I not only prefer a solution only in real numbers especially for our problem, but also believe that we are implicitly asked to prove the claim only in real numbers, but I accept the fact that the problem does not say so.
A solution which tries to avoid using "squaring" :
Let $t:=\sqrt{a+\sqrt x}\gt 0$, so $t^2=a+\sqrt x$.
$$(1)\iff x+t=a$$
Eliminating $a$, we get
$$x+t=t^2-\sqrt x\iff t^2-t-x-\sqrt x=0$$
Solving this for $t$ gives
$$t=\frac{1\pm \sqrt{(2\sqrt x+1)^2}}{2}=\frac{1\pm (2\sqrt x+1)}{2}=1+\sqrt x,-\sqrt x$$
Since $t\gt 0$, we get $$(t=)\ \ a-x=1+\sqrt x\tag3$$
Note that if $(3)$ has a solution, then $(1)$ has a solution since $$\sqrt{a+\sqrt x}=\sqrt{1+2\sqrt x+x}=1+\sqrt x=a-x$$
The rest is the same as the solution written at the top.