Bugs, starting at vertices of a square, chasing their counterclockwise neighbors: calculating total turn before they collide

Question

The following is from Art and Craft of Problem Solving, Paul Zeitz, third edition.

Example 3.1.6 and Problem 3.1.19

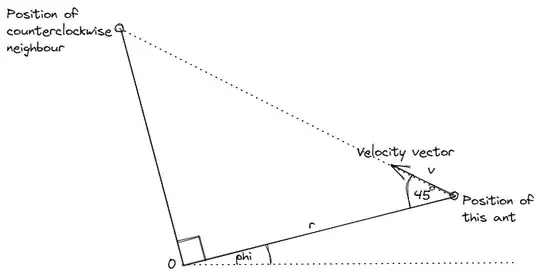
Four bugs are situated at each vertex of a unit square. Suddenly, each bug begins to chase its counterclockwise neighbor. As the bugs travel, they “turn”. For example, if one bug starts out facing due north, but then gradually comes to face due west, it will have turned $90^\circ$. It may even be that the bugs turn more than $360^\circ$. How much does each bug turn (in degrees) before they crash into each other?

I don't quite understand what is the question asking.

Is it not the case that each bug turns by $90$ degrees? Initially, suppose a particular bug faced north, at its neighbour, and then as time passed the bug continuously turned in order to ensure it always was facing the same neighbour, until it crashed into it at the centre of the square, where it would now be facing west.

So, the total "turn" equals $90$ degrees.

What am I missing?

*Okay, the solution in the Instructor's Manual is as follows: I found the solution: Can you please explain this to me: "There will be an infinite amount of rotation. Consider the situation after the bugs have each rotated 1 degree. They are now, as before, lying at four vertices of a square, with exactly the same situation as at the start, in terms of angular relationships. Except for scale, it would be impossible to tell if this was not the starting configuration. Hence the bugs will rotate yet another degree, and another, and another . . ."

Is the above a sound solution? I ask because, the author seems to be assuming that bugs would rotate even after crashing into each other. Am I right? Otherwise, who is to say there is no upper bound on the number of times the bugs rotate. In other words, the author seems to be assuming there would be an infinite number of "another degree, another degree..." and so on. But what if they crash into each other after a finite number of rotations?

Answer 1

You're right that bug must continuously turn so that it is always facing its counterclockwise neighbour. You're also right that the bug will collide with its neighbour when it reaches the centre of the square. But I don't think it's true that a bug that starts off facing north will be facing west when it reaches the centre of the square.

To work out how much the bug will have turned when it reaches the centre of the square, we'll have to calculate the trajectory of the bug.

I suggest we use polar coordinates for this problem. We'll take the origin of our coordinate system to be the centre of the square. We'll use $l$ to denote the length of a side of the square, and we'll use $v$ to denote the speed at which the bug runs.

Assuming that our bug starts off facing north, the bug's initial position in Cartesian coordinates is $(\frac{l}{2}, -\frac{l}{2})$. This is $r = \frac{l}{\sqrt 2}$, $\phi = -\frac{\pi}{4}$ in polar coordinates. (Note that I'm expressing the angle in radians, not degrees.)

To make progress, we need to write down some equations that describe how the bug moves over time. The key insight is the following: Since the bug is always facing its anticlockwise neighbour, the velocity vector of the bug always makes a $45^\circ$ angle to the displacement vector of the bug relative to the centre of the square. This sentence is hard to parse, so I suggest you look at the image below.

In polar coordinates, the radial and tangential components of the velocity vector are $\frac{dr}{dt}$ and $r\frac{d\phi}{dt}$ respectively. From what we said above, the radial component of the velocity vector is always equal to $-v\sin \frac{\pi}{4} = -\frac{v}{\sqrt{2}}$ and the tangential component of the velocity vector is always equal to $v\cos\frac{\pi}{4} = \frac{v}{\sqrt{2}}$. Thus \begin{align} \frac{dr}{dt} &= -\frac{v}{\sqrt{2}} \\ r\frac{d\phi}{dt} &= \frac{v}{\sqrt{2}}. \end{align}

The equation $\frac{dr}{dt} = -\frac{v}{\sqrt{2}}$, together with the initial condition $r|_{t = 0} = \frac{l}{\sqrt{2}}$, tells us that $$r = \frac{l}{\sqrt{2}} -\frac{v}{\sqrt{2}} t. $$

In particular, the bug reaches the centre of the square ($r = 0$) at time $$ T_{\text{collision}} = \frac{l}{v}.$$

Substituting the equation $r = \frac{l}{\sqrt{2}} -\frac{v}{\sqrt{2}} t $ into the equation $r\frac{d\phi}{dt} = \frac{v}{\sqrt{2}}$ gives $$ \frac{d\phi}{dt} = \frac{v}{l - vt}.$$

Integrating this, using the initial condition $\phi|_{t = 0} = -\frac{\pi}{4}$, gives $$ \phi = - \log \left( \frac{l - vt}{l} \right) -\frac{\pi}{4}.$$

Let's use $\Delta \phi$ to denote $\phi(t) - \phi|_{t = 0}$, the total angle through which that the bug has turned since the beginning of its journey. We have $$ \Delta \phi = - \log \left( \frac{l - vt}{l} \right). $$

Notice that $$ \lim_{t \to T_{\text{collision}}} \Delta \phi = \infty.$$ This means that, over the course of the bug's journey from the corner of the square to the centre of the square, the bug turns an infinite amount.