Can two geodesics meet tangentially on a Finsler manifold?

Question

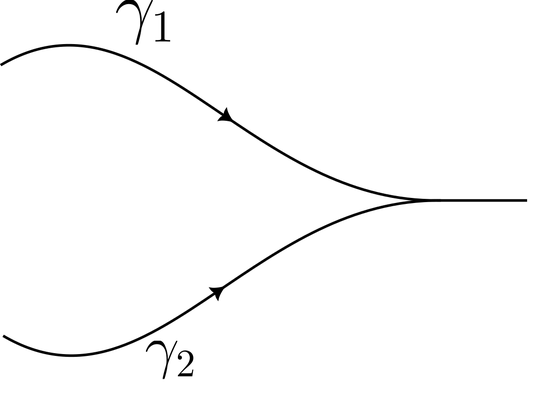
On a Riemannian manifold, it is well-known that two distinct non-closed geodesics can not meet tangentially, that is, if they meet at time $t_0$ and $t_1$, then they will meet at different angles. The proof uses the symmetric property of the Riemannian metric. As we do not have a symmetric property on a Finsler manifold, does the conclusion still hold? In other words, can we have a picture like the one below?

What do you think? How do you define geodesics? Finsler metrics? — Moishe Kohan, May 19 '23 at 02:16
@MoisheKohan A geodesic is a smooth curve that is locally distance minimizing, taking into account the non-symmetric nature of a Finsler metric. Explicitly, I am following the definition given in the book by Ohta Comaprison Finsler Geometry. — Sachchidanand Prasad, May 19 '23 at 04:01
I see, so you are not using the standard definition of a Finsler geodesic as in the book by Chern and Shen. Then my suggestion is to work out the geodesics in the plane with the standard $L^1$-metric. — Moishe Kohan, May 19 '23 at 04:09

score 2 · Accepted Answer · answered May 21 '23 at 03:58

Two distinct non-closed geodesics in a Finsler manifold must be transversal to each other. So the situation you mentioned cannot appear, even in a non-symmetric Finsler manifold.

Suppose $\gamma$ is geodesic for a Finlser metric $F$ on a manifold $M$. Then $\bar \gamma$, i.e, $\gamma$ traversed in the reverse direction is a geodesic for the reverse Finsler metric $\bar F$ (see, for example, Section 2.5 of Ohta's book).

Thus, if $\gamma_1$ and $\gamma_2$ meets tangentially, you must have $\bar \gamma_1$ and $\bar\gamma_2$ are identical. But that means $\gamma_1$ and $\gamma_2$ are identical.

Thank you! Your answer helped a lot! – Sujit Bhattacharyya Oct 29 '23 at 06:25 — Sujit Bhattacharyya, Oct 29 '23 at 06:25

Can two geodesics meet tangentially on a Finsler manifold?

1 Answers1