Does the following non-measurable function exist?

Question

Does there exist a function $f:[0,1]\to[0,1]$ such the graph of $f$ is dense in $[0,1]\times[0,1]$, and there exists a $M>0$ such for all $0<\epsilon_1,\epsilon_2 \le M$ and for all $0 < y_1 < 1$, if $0\le y_1-\epsilon_1< y_1< y_1+\epsilon_2 \le 1$ then the pre-image of $[y_1-\epsilon_1,y_1+\epsilon_2]$ under $f$ is non-measurable in the sense of Caratheodory?

If such a function exists, could we explictly define it?

I'm not sure how to proceed. Any suggestions would be great.

Attempt:

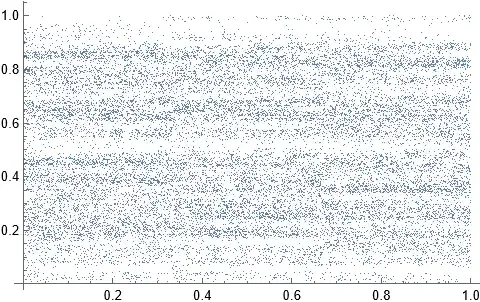
Someone gave my question a second chance. I have a function in mind but it's complicated to describe. I'm not sure the function gives what I want at the beggening of this post. My only evidence is a graph of countable points of the example at the end of the post.

I need a simpler function.

Suppose the base-$3$ expansion of real numbers, in interval $[x_1,x_2]$, have infinite decimals that approach $x$ from the right side so when $x_1=x_2$ we get $f(x_1)=f(x_2)$.

Furthermore, for $\mathbb{N}\cup\left\{0\right\}=\mathbb{N}_{0}$, if $r\in\mathbb{N}_{0}$ and $\text{digit}_{3}:\mathbb{R}\times \mathbb{Z}\to\left\{0,1,2\right\}$ is a function where $\text{digit}(x,r)$ takes the digit in the $3^{r}$-th decimal fraction of the base-$3$ expansion of $x$ (e.g. $\text{digit}_{3}(1.789,2)=\text{digit}_{3}({1.210022{\cdot\cdot\cdot}}_{3},2)=1$), then $\left\{{g_r}^{\prime}\right\}_{r\in\mathbb{N}_{0}}$ is a sequence of functions (and $\left[\cdot\right]$ is the nearest integer function) such that ${g_r}^{\prime}:\mathbb{N}_0\to\mathbb{N}_0$ is defined to be:

\begin{equation} g_r^{\prime}(x)=\left[\frac{10}{3}\sin(rx)+\frac{10}{3}\right] \end{equation}

then for some $k:\mathbb{N}\to\mathbb{R}$ where $k(0)$ is a positive number and $k$ is strictly increasing such if $x_1,x_2\in\mathbb{R}$, the intermediate function (before $f$) or $f_{1}:[0,1]\to[0,10]$ satisfies the problem at the beggenning of the post if the range is $[0,10]$ instead of $[0,1]$.

\begin{alignat}{2} & f_{1}(x) = &&\left|\left(\sum\limits_{r=0}^{\infty} g_{r+1}^{\prime}\!\left(\sum\limits_{p=r}^{r+k(r)}\text{digit}_{3}(x,p)\right)\!\!\bigg/3^{r}\right)-10\right|= \label{eq:025} \\ & && \left|\left(\left(\sum\limits_{r=0}^{\infty}\left[\frac{10}{3}\sin\left(\left(r+1\right)\left(\sum\limits_{p=r}^{r+k(r)}\text{digit}_{3}(x,p)\right)\right)+\frac{10}{3}\right]\right)\!\!\bigg /3^{r}\right)-10\right| \nonumber \end{alignat}

(One example of $k(r)$ that may satisfy the problem i.e. if the range is $[0,10]$, is $k(r)=10r+20$)

What we did was convert every digit of the base-$3$ expansion of $x$ to a pseudo-random number that is non-equally likely to be an integer, including and in-between, $0$ and $20/3$. Furthermore, we attempt to make the function dense in $[0,1]\times[0,10]$, by adding the $3^{r}$-th decimal fraction with the next $k$ decimal fractions; however, we want to control the end-points of $[0,10]$ such that $f_1$ is dense in $\left[0,1\right]\times\left[0,1\right]$ (instead of $\left[0,1\right]\times[0,10]$) by manipulating $f_1$ to get:

\begin{alignat}{2} & f(x) = && 1-\frac{1}{10}f_1(x)\label{eq:109}\\ & && 1-\left(\frac{1}{10}\right)\left|\left(\left(\sum\limits_{r=0}^{\infty}\left[\frac{10}{3}\sin\left(\left(r+1\right)\left(\sum\limits_{p=r}^{r+k(r)}\text{digit}_{3}(x,p)\right)\right)+\frac{10}{3}\right]\right)\!\!\bigg/3^{r}\right)-10\right| \nonumber \end{alignat}

(e.g. $k(r)=10r+20$) you can use programming to visualize $f$ though I don't know if you can graph the entire function. (The programming I used is mathematica.)

Clear["Global`*"]
k[r_] := k[r] = 
  20 (* You can adjust k[r]; however, mathematica is unable to graph \
f when k[r] is steepy increasing e.g. for this function, k[r] must be \
less than 25 for the code to show a graph. *)
g1[xr_, r_] := 
 g1[xr, r] = 
  Round[(10/3) Sin[r xr] + (10/
      3)] (Converts the (3^r)th decimal fraction,in the base 3 

expansion of the x-values in[x1,x2] (defined as xr or x_r not xr) 

into a psuedo-random number that's non-equally likely to spit a 

number between,and including, 0 and 20/3 *)
f[x_] := f[x] = 
  N[1 - ((1)/(10)) RealAbs[
      Sum[g1[Sum[
           RealDigits[x, 3, k[r], -r][[1]][[z]], {z, r + 1, k[r]}], 
          r + 1]/(3^r), {r, 0, 8}] - 
       10]] (Defines function f,I assume the larger k[r]'s values, the more 

the function appears dense in [0,1]x[0,1])
p = .00005 (Incremement between the x-values in the points of the 

graph below)
ListPlot[Table[{x, f[x]}, {x, p, 1, 
   p}]] (Graphs countable points of the functions but is not a 

complete accurate graph. There are uncountably many points that need 

to be included.)

Unfortunately, I only studied up to intro to advanced mathematics. This could be non-sense. (Without a deep undestanding of math I'm unable to prove if the function gives what I'm looking for.)

Is there a simpler example?

Answer 1

Very rough sketch:

1. Construct a Vitali set of outer-measure exactly $1$. Then $[0,1]$ can be written as the disjoint union $\bigcup_{n=1}^\infty V_n$ of countably many such sets. Note in particular that every $V_n$ is dense (this follows from having outer measure 1).

2. Verify that any nontrivial union of the $V_n$ (i.e. not empty and not all of $[0,1]$) is non-measurable. This should be clear because if $W = \bigcup_{n \in I} V_n$ where $\emptyset \ne I \subsetneq \mathbb{N}$, then the outer measure of $W$ is necessarily 1, but as long as the complement $[0,1] \setminus W$ contains at least one of the $V_n$, it too has outer measure 1.

3. Enumerate the rationals in $[0,1]$ as $\{q_n\}$. Define $f$ by $f(x) = q_n$ for $x \in V_n$. This is well-defined because the $V_n$ partition $[0,1]$.

4. To see that the graph of $f$ is dense in $[0,1] \times [0,1]$, note that for any small box $(a,b) \times (c,d)$ there exists $n$ with $q_n \in (c,d)$ (because the rationals are dense), and then we can find some $x \in V_n \cap (a,b)$ (because $V_n$ is dense). Hence the graph of $f$ intersects $(a,b) \times (c,d)$.

5. For any nontrivial interval $[c,d] \subset [0,1]$, we have $f^{-1}([c,d]) = \bigcup_{q_n \in [c,d]} V_n$ which is a nontrivial union of the $V_n$ and hence is non-measurable.

This is about as "explicit" an example as one can provide, because non-measurable functions can't be constructed without using the axiom of choice in an essential way.

I don't think the function $f$ in your example is non-measurable. Indeed, the functions $\operatorname{digit}_3$ and $g_r'$ are Borel functions, and the Borel function are closed under basic arithmetic operations and pointwise limits, including infinite series. Since your $f$ is defined using only such operations, it must be Borel, so in fact the preimage of every interval under $f$ is a Borel set and thus measurable.