I want to find decompose $\mathfrak{sl}_2$ as a direct sum of irreducible representations of $U(\mathfrak{sl}_2)$ which is the universal enveloping algebra of $\mathfrak{sl}_2$. I have a theorem that basically does the job for me by classifying all irreducible representations of $U(\mathfrak{sl}_2)$ saying for each $n\in \mathbb N^{*}$ there is a unique (up to iso) irreducible representation of dimension $n$ and the action of $U(\mathfrak{sl}_2)$ is given by 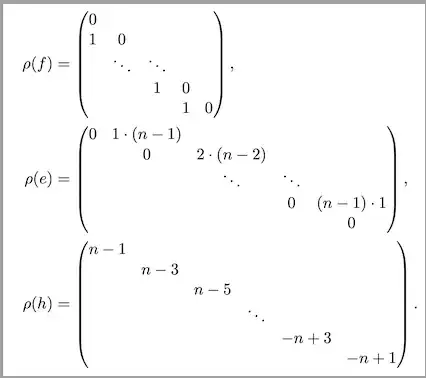
So to my understanding if it decomposes as $V_1\oplus V_2$ for $\dim V_1=1$ it means that there is a non zero element of $\mathfrak{sl}_2$ stable under the matrices (0),(0),(0) ($f,e,h$ in dimension 1), so we can take any element, say $e$.
Now for $V_2$ let's take $\operatorname{span}\{f,h\}$, we directly see that we have a problem since $[e,h]=-2e\notin V_2$, and I think we will get similar problems for other combinations or even if we don't chose $e$ so I'm misunderstanding something.
Here how can we decompose $\mathfrak{sl}_2$ into irreducible representations of $U(\mathfrak{sl}_2)$ ?