Consider the triangle ABC in which $AC(AB+ AC)={BC}^{2}$ Show that angles $BAC = 2\cdot ABC$.

Question

MY IDEAS

MY DRAWING

So I processed the equality that was given

$AC(AB+ AC)={BC}^{2}$

$AC=\frac{{BC}^{2}}{AB+AC}$

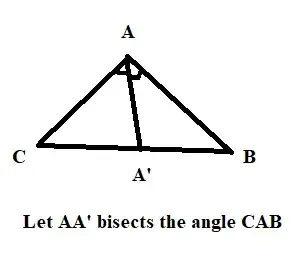
As you can see, I put a point AA' that bisects the angle CAB. I will apply the bisector theorem in triangle CAB with the bisector AA'.

$\frac{BA'}{A'C}=\frac{AB}{AC}$

$\frac{BA'+A'C}{A'C}=\frac{AB+AC}{AC}$

$\frac{BC}{A'C}=\frac{AB+AC}{AC}$

$AB+AC=\frac{BC\cdot AC}{A'C}$

Then we are switching $AB+AC$ with what we discover it equals.

${AC}^{2}\cdot BC={BC}^{2}\cdot A'C$

$AC=\sqrt{BC\cdot A'C}$

This seems like the reciprocal of the leg theorem. I don't know what to do forward.

All ideas are welcome. Hope one of you can help me. Thank you!

Does this answer your question? Finding a triangle angle based on side length equality - found using an Approach0 search. Although this proposed duplicate deals with a specific angle, i.e., $70^{\circ}$, the methods used in the answers there do not specifically rely on it being any specific value. Also, FYI, there are ... — John Omielan, May 01 '23 at 18:53
(cont.) several related AoPS threads, e.g., Geometry Problem :P, Find relation in triangle, etc. — John Omielan, May 01 '23 at 18:56

yanruijie · Accepted Answer · 2023-05-01T22:37:12.660

3

I propose a solution without trigonometric functions. As shown in the figure above, construct $D$ on $\overrightarrow{CA}$ such that $AD=AB$. Let $\angle BAC=2\alpha$, then we have $$\angle ADB=\angle ABD=\alpha\,.$$ From the given equation, we derive $$\frac{AC}{BC}=\frac{BC}{AB+AC}=\frac{BC}{AD+AC}=\frac{BC}{DC}\,,$$ and with $\angle ACB=\angle BCD$, it follows that $\triangle ACB\sim\triangle BCD$. Therefore, $$\angle ABC=\angle BDC=\alpha\,.$$ We conclude that $\angle BAC=2\angle ABC$.

edited May 01 '23 at 22:37

answered May 01 '23 at 22:11

yanruijie

620

1

Very creative solution. (+1) – Bob Dobbs May 01 '23 at 22:23

score 1 · Answer 2 · answered May 01 '23 at 18:51

Define: $A=\angle CAB, B=\angle ABC, C=\angle BCA$, by cosine law:

$$\cos A=\frac{AB^2+AC^2-BC^2}{2AB\cdot AC}=\frac{AB-AC}{2AC}$$

Next, by sine law:

$$\frac{AB}{AC}=\frac{\sin C}{\sin B}$$

Note $\sin C=\sin(A+B)$, So we get:

$$2\cos A=\frac{\sin(A+B)}{\sin B}-1$$

Multiply $\sin B$ on both sides and expand $\sin(A+B)=\sin A\cos B+\cos A\sin B$, we get:

$$\begin{align}\sin B&=\sin A\cos B-\cos A\sin B\\ \\ \sin B&=\sin(A-B)\\ \\ B&=A-B\\ \\ A&=2B\end{align}$$

score 1 · Answer 3 · answered May 01 '23 at 19:38

Maybe not the most efficient proof but I think this still works.

$$(AC)(AB+AC)=BC^2$$ $$\Rightarrow (AC)(AB+AC)(AB-AC)=BC^2(AB-AC)$$ $$\Rightarrow (AC)(AB^2-AC^2)=(BC^2)(AB-AC)$$ $$\Rightarrow (AC)(AB^2)-AC^3=(AB)(BC^2)-(AC)(BC^2)$$ $$\Rightarrow (AC)(AB^2)+(AC)(BC^2)-AC^3=(AB)(BC^2)$$ $$\Rightarrow AC\cdot\frac{AB^2+BC^2-AC^2}{(AB)(BC)}=BC$$ $$\Rightarrow AC\cdot\frac{AC^2-AB^2-BC^2}{-(AB)(BC)}=BC$$ $$\Rightarrow AC\cdot\frac{AC^2-AB^2-BC^2}{-2(AB)(BC)}=\frac{1}{2}BC$$

From the cosine rule $AC^2=AB^2+BC^2-2(AB)(BC)\cos(\angle ABC)\Rightarrow \cos(\angle ABC) = \frac{AC^2-AB^2-BC^2}{-2(AB)(BC)}$ we get

$$\Rightarrow AC\cdot \cos(\angle ABC)=\frac{1}{2}BC$$ $$\Rightarrow AC\cdot 2 \sin (\angle ABC)\cos(\angle ABC) =BC\cdot \sin(\angle ABC)$$ $$\Rightarrow AC\cdot \sin(2 \angle ABC) =BC\cdot \sin(\angle ABC)$$ $$\Rightarrow \frac{1}{2}(AB)(AC) \sin(2 \angle ABC) =\frac{1}{2}(AB)(BC)\cdot \sin(\angle ABC)$$

Then by construction the RHS is the area of the triangle $[\triangle ABC]$ which is also equal to $[\triangle ABC]= \frac{1}{2}(AB)(AC)\sin(\angle BAC)$ so we get

$$\frac{1}{2}(AB)(BC)\cdot \sin(\angle ABC)= [\triangle ABC]= \frac{1}{2}(AB)(AC)\sin(\angle BAC)=\frac{1}{2}(AB)(AC) \sin(2 \angle ABC)$$ Looking at the extreme right we have

$$\frac{1}{2}(AB)(AC)\sin(\angle BAC)=\frac{1}{2}(AB)(AC) \sin(2 \angle ABC)$$

$$\Rightarrow \angle BAC = 2 \angle ABC $$

Narasimham · Answer 4 · 2023-05-02T12:10:14.177

Using Sine Rule.

$\sin \alpha = s, \cos \alpha = c $ for short hand

we add 1 to denote side lengths. We also cancel $s$ common factor in the denominator

$$ \dfrac{a1}{2 c } =\dfrac{b1}{1}= \dfrac{c1}{3-4s^2} = D, \text{ related to Circle circum-diameter }$$

$$ b1= D, ~ a1= 2cD,~ c1= (4c^2-1) D $$ Eliminate D,C and simplify

$$ b1~ c1 = a1^2-b1^2 \tag1 $$ We need to prove $$ b1 (b1+c1)= a1^2 $$ or $$b1 ~ c1=a1^2- b1^2. \tag 2 $$

score 0 · Answer 5 · answered May 01 '23 at 20:25

COMMENT.-For short we note $AC=b$, $AB=c$ and $BC=a$ so the given relation becomes $$bc=a^2-b^2\tag 1$$ Angles $A$ and $B$ could be different for distinct realizations of such triangles but the relation $A=2B$ caracterizes the condition $(1)$. We have the two following examples with integer sides $$(a,b,c)=(20,16,9),(30,25,11)$$ which correspond to distinct angles $B$.

We can find without difficulty using $(1)$ $$\cos(A)=\frac{c-b}{2b}\text { and } \cos(B)=\frac{c+b}{2a}$$ and it remains to verify that $\cos(A)=2\cos^2(B)-1$ which it seems not hard usin again $(1)$.

Bob Dobbs · Answer 6 · 2023-05-01T22:34:24.490

Let $x=A'B$ and $y=AA'$. Then,

By using the interior angle bisector theorem $\frac{A'B}{BA}=\frac{A'C}{CA}$, we have $\frac{BC-x}{AC}=\frac{x}{AB}$ and thus $x=\frac{AB.BC}{AB+AC}$. It is given that $\frac{BC}{AB+AC}=\frac{AC}{BC}$. Therefore, $x=\frac{AB.AC}{BC}$.
By using the interior angle bisector length theorem $AA'^2=AB.AC\left(1-\left(\frac{BC}{AB+AC}\right)^2\right)$, we get $y^2=\frac{AB.AC}{BC^2}(BC^2-AC^2).$
You got $AC=\sqrt{BC.A'C}$. This gives $BC^2-AC^2=BCx$.
If we use 3 in 2, we get $y^2=\frac{AB.AC}{BC}x.$
If we use 1 in 4, we get $y^2=x^2$. Hence $x=y$ and $\angle A'AB=\angle A'BA$ which implies $$\angle BAC=2\angle ABC.$$

Consider the triangle ABC in which $AC(AB+ AC)={BC}^{2}$ Show that angles $BAC = 2\cdot ABC$.

6 Answers6