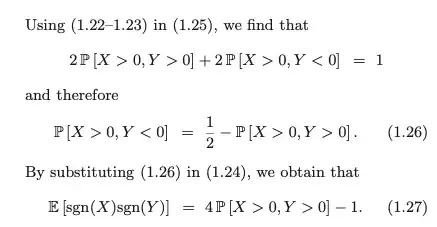5

The following question is from the book: "150 Most Frequently Asked Questions on Quant Interviews" By Stefanica, Radoicic, and Wang.

Let $X$ and $Y$ be standard normal variables with joint normal distribution with correlation $\rho$.

Find the expectation

$$ \mathbb E [\text{sgn}(X )\text{sgn}(Y )]$$

where $\text{sgn}(·)$ is the sign function given by $\text{sgn}(x) = 1$, if $x > 0$, $\text{sgn}(x) = −1$, if $x < 0$, and $\text{sgn}(0) = 0$.

My Approach

Now, my first instinct was to write out the formula for the correlation in terms of expectations and see where to go from there. So for readability, using $X = \text{sgn}(X)$ and $Y = \text{sgn}(Y)$:

$$ \rho_{XY} = \dfrac{\text{Cov}(X,Y)}{\sigma_X \sigma_Y} = \dfrac{\mathbb E[XY] - \mathbb E[X]\mathbb E[Y]}{\sigma_X\sigma_Y} $$

from there, I was able to intuit that the means of $X$ and $Y$ are zero. Nothing really changes if you take the sign of a standard normal distribution instead of the value right? They're both symmetric around zero?

So I simplified the above fraction to:

$$ \rho_{XY} = \dfrac{\mathbb E[XY]}{\sigma_X\sigma_Y} $$

So next was to find the standard deviations, the formula for which is:

$$ \sigma_X = \sqrt{\frac{1}{n} \sum_i^n (x_i - \bar{X})^2} $$

And if we know $\bar{X} = 0$, then the variance's for both is 1?

Which leads me to the solution:

$$ \mathbb E[XY] = \rho_{XY}$$

Which when I checked the book's solution, is utterly wrong. There is a deterministic solution...

Why Am I Wrong?

This is really what I'm trying to reach. This is practice for interviews, so I don't care about knowing the answer, I want to learn how to tackle problems such as these.

Here's where I think I went wrong: the expectation is not zero? I think the correlation twists the expectation here. I think my answer only works when they are independent, which doesn't help... But I thought I did the math right? This is where I'm lost.

Sanity check for why I'm wrong:

  • If $\rho=-1$, then $\mathbb E[XY] = -1$

  • If $\rho=1$, then $\mathbb E[XY] = 1$

The solution confirms this...

The Book's Solution

The book has a three-page long derivation which simplifies to $\frac{\pi}{2}$ that I honestly don't understand.

It starts off with assuming $\rho=1$ or $\rho=-1$ and reaching the conclusion that $E \in [-1,1]$, which is what I have above. So at least I have that part correct...

First section of the book's solution

It then goes on to break down the expectation by the 2x2=4 possible combinations of values for $X,Y$, then uses the fact that all four spaces sum up to 1 to boil down the problem into a simple formula, dependent on $\mathbb{P}[X > 0, Y> 0]$ (1.27):

breaking down the problem, pic1 breaking down the problem, pic 2

I don't think I would've done this, but OK. So far so good. It then assumes an identity/transformation that I've never seen before, with notation I've never seen before either (1.28):

enter image description here

Which then uses polar coordinates and change of variables to solve the integral:

enter image description here enter image description here

At which point, I'm completely lost. This seems like a hard problem right? Definitely not one I'd see in an interview.

My question is: is there a simpler way to understand how to tackle this problem? Seems like it's way too complicated. If not, is there a more visual way to understand this? I know that two standard normal RV's can be visualized in a 2D grid so that their distributions are symmetric around the origin. Not sure how that translates to when they're correlated or their sign version is

The last few equations seem to imply some level of circular intuition behind the solution.. so can anyone help provide some clarity? My problem really is once I saw the identity that I didn't know I completely lost track of the problem in my head, and don't think I could've recreated the solution after that...

Thanks

Math Attack
  • 5,343
Joe
  • 563
  • 3
    Using standard deviation's statistical formula is a red flag for me. The probabilistic standard deviation and the standard deviation of data points, these are not the same necessarily. Also, whenever you say: ".. should be ... right?" stop and make yourself prove it. If you have difficulty proving a particular point, it may be because your intuition was wrong - and human intuition is often wrong with probability. – FShrike Apr 26 '23 at 19:48
  • 4
    A lot of interview questions are to see how you approach a problem and whether you have a good intuition about the traps that might appear. The interviewer may not even expect you to be able to solve it there. – Brian Moehring Apr 26 '23 at 20:00
  • 1
    @BrianMoehring +1, exactly, - you ask a hard problem to see how a person thinks, and then guide them with hints and/or push them forward as appropriate – gt6989b Apr 26 '23 at 20:03
  • 1
    It is a nice interview question. If I was the interviewer I'd expect the candidate only to come up with the idea that $X$ can be expressed as $X=\rho Y+\sqrt{1-\rho^2}Z$ where $Y$ and $Z$ are independent. The rest is boring homework math and you want to ask the candidate further questions in, say, the rest of that hour. – Kurt G. Apr 27 '23 at 07:09
  • If I were the interviewee I'd be crying (: – Joe Apr 28 '23 at 01:14
  • 1
    By the way, there's nothing wrong with $\mathbb{E}(XY) = \rho_{XY}$, but importantly $\rho_{XY} \neq \rho$, so the whole question is still "What is $\rho_{XY}$?" (To avoid this confusion, never write something like $X=\text{sgn}(X)$ unless it's true) – Brian Moehring Apr 28 '23 at 20:48
  • fair point, i tend to make that mistake a lot... – Joe May 03 '23 at 15:14

0 Answers0