Consider a particular solution to a diffusion equation:
$$\frac{\partial^2}{\partial t^2}\Phi(x,t)=-\frac{x}{t}\frac{\partial}{\partial x}\Phi(x,t)$$
which is:
$$ \Phi(x,t)=\exp \frac{t}{\log x}. $$
I wish to construct a space curve, that over time, traces out a surface $M \subset (0,1)^3$ homeomorphic to $(0,1)\times S^1 $ and orthogonally projects onto the distributional solution $\forall t \in (1/3,3)$, augmented by the fact that $\Phi$ is decorated on the $xy, zy, zx$ planes with $x,y,z \in (0,1).$ Just to be clear $M$ must be an open cylinder that accumulates to $p=(0,1,1)$ and $q=(1,0,0)$ to satisfy the projective and topological conditions.
In the case where one drops the projective condition but enforces the topological condition, one sees that the cylinder is homeomorphic to an annulus and a once punctured plane. Therefore, the projective condition rigidifies the geometry of $M.$
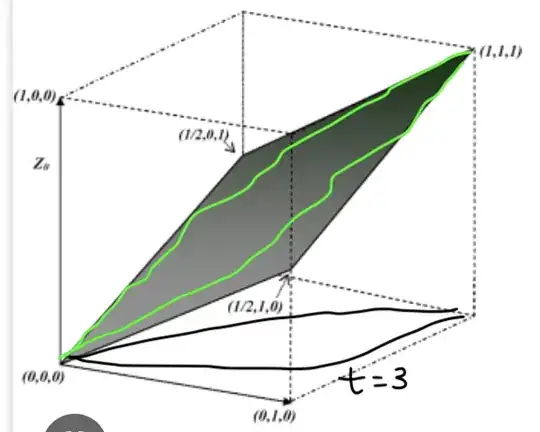
It's clear that one can lift the finite subset of projection curves i.e. for $t=1/3,3$ onto the surface essentially associating a skeleton to the surface, $\mathrm{Skel}(M).$ Then one can define the non-smooth convex surface $N$ as an approximator to $M$ by connecting $\mathrm{Skel}(M)$ by straight line segments. In this way, one obtains a geometric structure comprised of $4,$ $1$-cells and $4,$ $2$-cells. The objective is reduced to smoothly interpolating $\mathrm{Skel}(M)$ while satisfying the projective conditions.
The above image depicts (not to scale) the planar projection curves for $t=1/3,3$ and their lift (green curves) onto the template (dark grey plane). This constitutes $2$ out of $4$ curves in the finite set $\mathrm{Skel}(M).$ To complete the set just take a plane orthogonal to the existing plane and lift another $2$ projection curves onto that template.
How do you smoothly interpolate $\mathrm{Skel}(M)$ while satisfying the projective conditions? Is there an explicit parametrisation of $M?$
Can it be done with a rotational homotopy?
See this answer here for how it can be done in a more symmetric case (reflectional symmetry of the base curves). Unfortunately I don't have this symmetry with $\Phi$.