When computing spectral moments of the sample correlation matrix (Wishart matrices), as described here there is a need to integrate over the orientation of eigenvectors of the matrix in question. This can be accomplished by computing a following density of states as defined below. Before defining the quantity in question let us write down some auxiliary quantities.
Let $N \ge 2$ be an integer and let $L:= diag(l_j)_{j=1}^N$ and $\Sigma := diag(s_j)_{j=1}^N $ be two diagonal square matrices with non-negative entries. Then let $O$ be an orthogonal matrix of dimension $N \times N$. It is well known that such a matrix is uniquely parametrized by $\binom{N}{2}$ angles $\vec{\alpha}:= \left( \alpha_j \right)_{j=1}^{\binom{N}{2}}$ each of which running from zero to two pi. For example, if $N=3$, the matrix $O$ reads:
\begin{equation} O= \left( \begin{array}{ccc} \cos \left(\alpha _1\right) & -\sin \left(\alpha _1\right) & 0 \\ \sin \left(\alpha _1\right) & \cos \left(\alpha _1\right) & 0 \\ 0 & 0 & 1 \\ \end{array} \right)\cdot \left( \begin{array}{ccc} \cos \left(\alpha _2\right) & 0 & -\sin \left(\alpha _2\right) \\ 0 & 1 & 0 \\ \sin \left(\alpha _2\right) & 0 & \cos \left(\alpha _2\right) \\ \end{array} \right) \cdot\left( \begin{array}{ccc} 1 & 0 & 0 \\ 0 & \cos \left(\alpha _3\right) & -\sin \left(\alpha _3\right) \\ 0 & \sin \left(\alpha _3\right) & \cos \left(\alpha _3\right) \\ \end{array} \right) \end{equation}
Now we define other quantities as ${\mathfrak A}_j(\vec{\alpha}) := @[l_j] \left[ Tr \Sigma^{-1} \cdot O \cdot L \cdot O^T\right]$ for $j=1,\cdots, N$. In other words the $j$th quantity is the coefficient at $l_j$ of the trace of the product of matrices as given in the last sentence. At this point we are ready to define our density of states. Let $\kappa:=\binom{N}{2}$ and then we have:
\begin{equation} \omega\left( A_1,\cdots,A_{N-1} \right) := \int\limits_{[0,2 \pi]^\kappa} \prod\limits_{j=1}^{N-1} \delta \left( A_j - {\mathfrak A}_j(\vec{\alpha}) \right) d^\kappa \vec{\alpha} \tag{1} \end{equation}
Now, what has been accomplished. We , almost, computed the quantity in $(1)$ for $N=3$. We firstly state the result and then we state how it was being obtained. Here we go:
\begin{eqnarray} &&\left. \omega\left( A_1,A_2 \right) = \right. \\ && \left. 4 \sqrt{s_1 s_2} s_3 \cdot \right. \\ && \left. \int\limits_{\cdots}^{\cdots} d\alpha_2 \right. \\ && \left. \frac{1}{ \sqrt{\left(A_1+\left(\frac{1}{s_3}-\frac{1}{s_2}\right) \cos ^2\left(\alpha _2\right)-\frac{1}{s_3}\right) \left(-A_1+\left(\frac{1}{s_1}-\frac{1}{s_3}\right) \cos ^2\left(\alpha _2\right)+\frac{1}{s_3}\right)} } \cdot \right. \\ && \left. \frac{1}{ % \sqrt{-A_2 \left(A_1+A_2\right) s_1 s_2 s_3^2+A_1 s_1 s_2 s_3+A_2 s_3 \left(s_1 s_2+s_3 s_2+s_1 s_3\right)+\left(s_1-s_3\right) \left(s_2-s_3\right) \cos ^2\left(\alpha _2\right)-s_3^2-s_1 s_2}} % \right. \tag{2} \end{eqnarray}
where the limits of integration are such that $\alpha_2 \in [0,2 \pi]$ and that the quantities in the square roots in the denominators are non-negative. It wouldn't be hard to find those limits explicitly.
The result was obtained by simply using the properties of the Dirac delta function. We enclose the Mathematica code that was being used for this purpose.
In[56]:= (* Orthogonal group in N dimensions. Take N>3 *)
NN = 3; p = 2; Clear[s];
Clear[a];
OO = Table[0, {NN (NN - 1)/2}]; count = 1;
Do[
Do[
OO1 = IdentityMatrix[NN];
{{OO1[[i, i]], OO1[[i, j]]}, {OO1[[j, i]],
OO1[[j, j]]}} = {{Cos[a[count]], -Sin[a[count]]}, {Sin[a[count]],
Cos[a[count]]}};
OO[[count]] = OO1;
count ++;
, {j, i + 1, NN}]
, {i, 1, NN}]
MatrixForm[#] & /@ OO;
H = Dot @@ OO;
L = DiagonalMatrix[Table[l[j], {j, 1, NN}]];
Sigma1 = DiagonalMatrix[Table[1/s[j], {j, 1, NN}]];
As = Table[
Collect[Coefficient[TrigReduce[Tr[Sigma1.H.L.Transpose[H]]],
l[j]], {Cos[_], Sin[_]}, Simplify], {j, 1, NN}];
MatrixForm[As];
((MatrixForm[#]&/@OO/.{a[j_][RuleDelayed]
Subscript[[Alpha],j]})//TeXForm)
In[85]:= (Define As[[j]] as the coefficient at l[j] in
Tr[Sigma^(-1).H.L.Transpose[H]]. Use code snippet above to generate
those As. )
(We know that Sum[As[[j]],{j,1,NN}] [Equal] Tr[ Sigma^(-1) ] =
Const[ a[j]]. Therefore there are only NN-1 independent As.)
(* Here we simplify those independent As.)
Clear[mD]; nn1 =.; nn2 =.; nn3 =.; x =.; A =.; fT1 =.; fT2 =.; cT1
=.; cT2 =.; xbA =.; A1 =.; A2 =.;
nn10 =.; nn11 =.; nn20 =.; nn21 =.; nn31 =.;
()
msubst00 = {fT1 :> (1/s[1] + 1/s[2] + 2/s[3]),
fT2 :> (3/s[1] + 3/s[2] + 2/s[3]),
cT1 :> (1/s[1] + 1/s[2] - 2/s[3]), cT2 :> (1/s[1] - 1/s[2])};
(The density of states in question is a product of Dirac Delta
functions evaluated at those two expressions in parentheses below.)
{fT1, fT2, cT1,
cT2} = {(1/s[1] + 1/s[2] + 2/s[3]), (3/s[1] + 3/s[2] + 2/s[3]), (1/
s[1] + 1/s[2] - 2/s[3]), (1/s[1] - 1/s[2])};
(As[[1]] - 1/4 ( fT1 + Cos[2 a[2]] cT1) -
1/4 cT2 (1 + Cos[2 a[2]] ) Cos[2 a[1]]) // Simplify
(As[[2]] - 1/8 fT2 -
1/8 cT1 ( Cos[2 a[2]] Cos[2 a[3]] + Cos[2 a[3]] - Cos[2 a[2]] ) -
1/8 cT2 (
Cos[2 a[1]] (-1 - Cos[2 a[2]] - 3 Cos[2 a[3]] +
Cos[2 a[2]] Cos[2 a[3]]) +
4 Sin[2 a[1]] Sin[a[2]] Sin[2 a[3]]) ) // Simplify
(Now we use Identity 1 above to evaluate the integral over a[1] \in
[0, 2Pi] .)
(The quantity md[] below is a Dirac Delta.*)
Clear[mD]; nn1 =.; nn2 =.; nn3 =.; x =.; A =.; fT1 =.; fT2 =.; cT1
=.; cT2 =.; xbA =.; A1 =.; A2 =.;
nn10 =.; nn11 =.; nn20 =.; nn21 =.; nn31 =.;
msubst0 = {x :> A1 - 1/4 ( fT1 + Cos[2 a[2]] cT1),
A :> 1/4 cT2 (1 + Cos[2 a[2]] )};
msubst01 = (xbA -> x/A /. msubst0) // Simplify;
msubst1 = {nn10 :> (A2 - 1/8 fT2 + 1/8 cT1 Cos[2 a[2]]),
nn11 :> -(1/8) cT1 ( Cos[2 a[2]] + 1)};
msubst2 = {nn20 :> -(1/8) cT2 (-1 - Cos[2 a[2]]),
nn21 :> -(1/8) cT2 (-3 + Cos[2 a[2]] )};
msubst3 = {nn31 :> -(1/2) cT2 Sin[a[2]]};
msubst = {nn1 :> nn10 + nn11 Cos[2 a[3]],
nn2 :> nn20 + nn21 Cos[2 a[3]], nn3 :> nn31 Sin[2 a[3]]};
((mD[nn1 + nn2 xbA + nn3 Sqrt[1 - xbA^2]] +
mD[nn1 + nn2 xbA - nn3 Sqrt[1 - xbA^2]] )/(
Abs[A] Sqrt[1 - xbA^2]));
(Now we do an integration over a[3] \in [0,2 Pi])
(It is simple. We just have a sum of two Dirac Delta's each of which
is evaluated at a linear combination of unity, then Cos[2 a[3]] and
then Sin[2 a[3]]. )
(1/(Abs[A] Sqrt[
1 - xbA^2]) (mD[
Collect[(nn1 + nn2 xbA + nn3 Sqrt[1 - xbA^2]) /.
msubst, {Cos[2 a[3]], Sin[2 a[3]]}, Simplify]] +
mD[Collect[(nn1 + nn2 xbA - nn3 Sqrt[1 - xbA^2]) /.
msubst, {Cos[2 a[3]], Sin[2 a[3]]}, Simplify]] ));
(Now we use Identity 2 above.)
res = 1/(Abs[A] Sqrt[1 - xbA^2]) (4/
Sqrt[(nn11 + nn21 xbA)^2 + (nn31 Sqrt[1 - xbA^2])^2 - (nn10 +
nn20 xbA)^2]);
res = Simplify[
res /. msubst0 /. msubst01 /. msubst1 /. msubst2 /. msubst3,
Assumptions -> 0 <= a[2] <= 2 Pi && Element[cT2, Reals]];
res = Simplify[res /. msubst00,
Assumptions ->
0 <= a[2] <= 2 Pi && s[1] >= 0 && s[2] >= 0 && s[3] >= 0];
Out[89]= 0
Out[90]= 0
In[118]:=
res1 = (4 Sqrt[s[1] s[2]]
s[3] )/([Sqrt](Cos[a[2]]^2 (s[1] - s[3]) (s[2] -
s[3]) - (s[1] s[2] + s[3]^2) + -s[1] s[2] s[
3]^2 A2 (A1 + A2) + A1 s[1] s[2] s[3] +
A2 s[3] (s[1] s[2] + s[1] s[3] + s[2] s[3])) [Sqrt](!(
*SubsuperscriptBox[([Product]), (xi =
0), (1)]((If[xi == 0, (-1)/s[2] + 1/s[3],
1/s[1] - 1/s[3]] Cos[a[2]]^2 + ((2\ xi -
1)) ((1/s[3] - A1))))) ));
ma2 = RandomReal[{0, 2 Pi}, WorkingPrecision -> 50];
mss = RandomReal[{0, 5}, 3, WorkingPrecision -> 50];
{mA1, mA2} = RandomReal[{-5, 5}, 2, WorkingPrecision -> 50];
(res - res1) /. a[2] :> ma2 /. {s[1] :> mss[[1]], s[2] :> mss[[2]],
s[3] :> mss[[3]]} /. {A1 :> mA1, A2 :> mA2}
Out[122]= 0.*10^-49
(res1 /. s[j_] :> Subscript[s, j] /.
a[j_] :> Subscript[[Alpha], j] /. {A1 :> Subscript[A, 1],
A2 :> Subscript[A, 2]})
Now , having said all that, my question would be the following. Firstly, how do we do the remaining integration over $\alpha_2$ in $(2)$ to obtain a closed form expression and secondly, a more ambitious question, can we obtain similar results for $N > 3$ as well?
Update 1 :
Now take $0 \le s_3 \le s_2 \le s_1$. Then the density is given as below:
\begin{eqnarray} &&\left.\omega(A_1,A_2):=\right. \\ &&\left. 4 \sqrt{s_1 s_2} s_3 \right. \\ &&\left. \int\limits_{ \zeta_-(A_1,A_2)}^{\zeta_+(A_1,A_2)} \frac{1}{\sqrt{\left(A_1+\left(\frac{1}{s_3}-\frac{1}{s_2}\right) \cos ^2\left(\alpha _2\right)-\frac{1}{s_3}\right) \left(-A_1+\left(\frac{1}{s_1}-\frac{1}{s_3}\right) \cos ^2\left(\alpha _2\right)+\frac{1}{s_3}\right)}}\right. \\ &&\left. \frac{1}{\sqrt{-A_2 \left(A_1+A_2\right) s_1 s_2 s_3^2+A_1 s_1 s_2 s_3+A_2 s_3 \left(s_1 s_2+s_3 s_2+s_1 s_3\right)+\left(s_1-s_3\right) \left(s_2-s_3\right) \cos ^2\left(\alpha _2\right)-s_3^2-s_1 s_2}} d \alpha_2 \right. \tag{4} \end{eqnarray}
where $1/s_1 \le A_1 \le 1/s_3$ and $1/s_1 + 1/s_2 - A_1 \le A_2 \le 1/s_3$ if $A_1 \in (1/s_1,1/s_2)$ and $1/s_1\le A_2 \le 1/s_2 + 1/s_3 -A_1$ if $A_1 \in (1/s_2,1/s_3)$.
The integration limits read:
\begin{eqnarray} &&\zeta_-(A_1,A_2) := \cos ^{-1}\left(\sqrt{\min \left(1,\frac{\frac{1}{s_3}-A_1}{\frac{1}{s_3}-\frac{1}{s_2}}\right)}\right)\\ &&\zeta_+(A_1,A_2) := \cos ^{-1}\left(\sqrt{\max \left(0,\frac{\frac{1}{s_3}-A_1}{\frac{1}{s_3}-\frac{1}{s_1}},\frac{A_2 \left(A_1+A_2\right) s_1 s_2 s_3^2-A_1 s_1 s_2 s_3-A_2 \left(s_1 s_2+s_3 s_2+s_1 s_3\right) s_3+s_3^2+s_1 s_2}{\left(s_1-s_3\right) \left(s_2-s_3\right)}\right)}\right) \end{eqnarray}
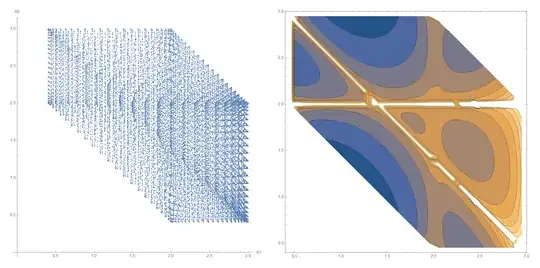
Now, we took $(s_1,s_2,s_3)=(5/2,1/2,1/3)$ and we plotted the quantity in $(4)$ (right) along with the scatter-plot of the respective mapping from the cube to the plane (left). Here we go:
(*Analytically.*)
lowLim[A1_, A2_, s_] :=
ArcCos[Sqrt[Min[(-A1 + 1/s[[3]])/(-1/s[[2]] + 1/s[[3]]), 1]]];
upLim[A1_, A2_, s_] :=
ArcCos[Sqrt[
Max[0, (-A1 + 1/s[[3]])/(-1/s[[1]] + 1/s[[3]]), (
s[[1]] s[[2]] - A1 s[[1]] s[[2]] s[[3]] + s[[3]]^2 +
A2 (A1 + A2) s[[1]] s[[2]] s[[3]]^2 -
A2 s[[3]] (s[[1]] s[[2]] + s[[1]] s[[3]] + s[[2]] s[[3]]))/((s[[
1]] - s[[3]]) (s[[2]] - s[[3]]))]]];
mDensity[A1_, A2_, s_] :=
NIntegrate[(4 Sqrt[s[[1]] s[[2]]]
s[[3]])/(Sqrt[(A1 + Cos[a[2]]^2 (-(1/s[[2]]) + 1/s[[3]]) - 1/
s[[3]]) (-A1 + Cos[a[2]]^2 (1/s[[1]] - 1/s[[3]]) + 1/
s[[3]])] \[Sqrt](-s[[1]] s[[2]] +
Cos[a[2]]^2 (s[[1]] - s[[3]]) (s[[2]] - s[[3]]) +
A1 s[[1]] s[[2]] s[[3]] - s[[3]]^2 -
A2 (A1 + A2) s[[1]] s[[2]] s[[3]]^2 +
A2 s[[3]] (s[[1]] s[[2]] + s[[1]] s[[3]] +
s[[2]] s[[3]]))), {a[2], lowLim[A1, A2, s],
upLim[A1, A2, s]}];
dA = 1/20; mim = 600;
Clear[s]; s = {5/2, 1/2, 1/3};
t0 = TimeUsed[];
mden1 = Flatten[
Table[{A1, A2, mDensity[A1, A2, s]}, {A1, 1/s[[1]], 1/s[[2]],
dA}, {A2, 1/s[[1]] + 1/s[[2]] - A1, 1/s[[3]], dA}], 1];
mden2 = Flatten[
Table[{A1, A2, mDensity[A1, A2, s]}, {A1, 1/s[[2]], 1/s[[3]],
dA}, {A2, 1/s[[1]], 1/s[[2]] + 1/s[[3]] - A1, dA}], 1];
Print["Computing density done in t0=", TimeUsed[] - t0];
mden = Join[mden1, mden2];
mden1 = Select[mden, NumberQ[#[[3]]] == True &];
pl2 = ListContourPlot[{#[[1]], #[[2]], Log[#[[3]]]} & /@ mden1,
ImageSize :> mim];
(Numerically.)
Clear[s]; {s[1], s[2], s[3]} = {5/2, 1/2, 1/3};
mygrid = Flatten[
Array[{#1, #2, #3} &, {50, 50,
50}, {{0, 2 Pi}, {0, 2 Pi}, {0, 2 Pi}}], 2];
myvals = Map[{1/4 Cos[2 #[[1]]] (1/s[1] - 1/s[2]) +
1/8 Cos[2 #[[1]] - 2 #[[2]]] (1/s[1] - 1/s[2]) +
1/8 Cos[2 #[[1]] + 2 #[[2]]] (1/s[1] - 1/s[2]) +
1/4 Cos[2 #[[2]]] (1/s[1] + 1/s[2] - 2/s[3]) +
1/4 (1/s[1] + 1/s[2] + 2/s[3]),
1/32 Cos[2 #[[1]] - 2 #[[2]] - 2 #[[3]]] (1/s[1] - 1/s[2]) +
1/32 Cos[2 #[[1]] + 2 #[[2]] - 2 #[[3]]] (1/s[1] - 1/s[2]) +
1/32 Cos[2 #[[1]] - 2 #[[2]] + 2 #[[3]]] (1/s[1] - 1/s[2]) +
1/32 Cos[2 #[[1]] + 2 #[[2]] + 2 #[[3]]] (1/s[1] - 1/s[2]) +
1/8 Cos[2 #[[1]]] (-(1/s[1]) + 1/s[2]) +
1/16 Cos[2 #[[1]] - 2 #[[2]]] (-(1/s[1]) + 1/s[2]) +
1/16 Cos[2 #[[1]] + 2 #[[2]]] (-(1/s[1]) + 1/s[2]) +
3/16 Cos[2 #[[1]] - 2 #[[3]]] (-(1/s[1]) + 1/s[2]) +
3/16 Cos[2 #[[1]] + 2 #[[3]]] (-(1/s[1]) + 1/s[2]) +
1/16 Cos[2 #[[2]] - 2 #[[3]]] (1/s[1] + 1/s[2] - 2/s[3]) +
1/8 Cos[2 #[[3]]] (1/s[1] + 1/s[2] - 2/s[3]) +
1/16 Cos[2 #[[2]] + 2 #[[3]]] (1/s[1] + 1/s[2] - 2/s[3]) +
1/8 Cos[2 #[[2]]] (-(1/s[1]) - 1/s[2] + 2/s[3]) +
1/8 (3/s[1] + 3/s[2] + 2/s[3]) +
1/8 (-(1/s[1]) + 1/s[2]) Sin[2 #[[1]] - #[[2]] - 2 #[[3]]] +
1/8 (1/s[1] - 1/s[2]) Sin[2 #[[1]] + #[[2]] - 2 #[[3]]] +
1/8 (1/s[1] - 1/s[2]) Sin[2 #[[1]] - #[[2]] + 2 #[[3]]] +
1/8 (-(1/s[1]) + 1/s[2]) Sin[2 #[[1]] + #[[2]] + 2 #[[3]]]} &,
mygrid];
pl1 = ListPlot[myvals, ImageSize :> mim, AxesLabel :> {"A1", "A2"},
AspectRatio -> 1];
GraphicsGrid[{{pl1, pl2}}]
Again, as we can see, the match is good.