A special point of a triangle related to the nine point circle

Question

Playing with the nine point circle in GeoGebra, I have "discovered" a special point.
I assume it is a well known point, but I cannot find its name and properties.

Description:

Let $ABC$ be a triangle with sides $a,b,c$,
$M_a, M_b, M_c$ are the midpoints of $a,b,c$,
$H_a,H_b,H_c$ the feet of the altitudes,
and $O$ the center of the nine point circle of $ABC$.

Let $N_a, N_b, N_c$ be the reflections of $H_a, H_b, H_c$ across $O$ (lying on the nine point circle).

Then the three straight lines connecting $A,B,C$ and $N_a, N_b, N_c$ intersect at a point $N$.

Using online geometric tools it is easy to check the following properties of the point $N$:

• $N$ exists if only $ABC$ is not a right triangle
• $N$ coincides with $O$ if only $ABC$ is an equilateral triangle
• $N$ coincides with one of $A$, $B$, or $C$ if only the corresponding angle is $45^\circ$ or $135^\circ$
• $N$ belongs to either the area of $ABC$, or one of the opposite angles of $A$, $B$, or $C$
• $N$ never lies on a side of $ABC$, except for the vertices $A$, $B$, and $C$

Questions:

1. How to prove the three straight lines connecting $A,B,C$ and $N_a, N_b, N_c$ intersect at a single point?
2. What is the name and what are the properties of the point $N$?

Answer 1

The solution I am going to write here is not probably beautiful but it indeed shows that $AN_a$, $BN_b$, and $CN_c$ are concurrent.

---

First of all, WLOG, we assume $C=(0,1)$, $B=(a,0)$, and $A=(-b,0)$, where $b$ is a positive real number.

---

Before going into the main body of the solution, we can easily note that the construction of your problem (or your image) proves the fact that $O$ is the midpoint of the line connecting the orthocenter and the circumcenter of the triangle, which is well-known though.

---

The orthocenter is the intersection of the lines $x=0$ and $y=a(x+b)$ (the line perpendicular to $CB$ and passing through $A$) So, the orthocenter is:

$$(0,ab ).$$

Similarly, the circumcenter is the intersection of the lines $x=\frac{a-b}{2}$ and $y-\frac{1}{2}=a(x-\frac{a}{2})$ (perpendicular bisector of $BC$). So, the circumcenter is:

$$(\frac{a-b}{2},\frac{1-ab}{2}).$$

Therefore, for the center of the nine-point circle, we have:

$$O=(\frac{a-b}{4},\frac{1+ab}{4}).$$

Now, we can easily compute:

$$H_c=(0,0), \\ H_a=(\frac{a(1-ab)}{1+a^2}, \frac{a(a+b)}{1+a^2}), \\ H_b=(\frac{b(ab-1)}{1+b^2}, \frac{b(a+b)}{1+b^2}).$$

And, considering the reflection with respect to $O$, we have (the computations are really simple):

$$N_c=(\frac{a-b}{2},\frac{1+ab}{2}), \\ N_a= (\frac{(a^2-1)(a+b)}{2(1+a^2)}, \frac{(a^2-1)(ab-1)}{2(1+a^2)}),\\ N_b= (\frac{(1-b^2)(a+b)}{2(1+b^2)}, \frac{(1-b^2)(1-ab)}{2(1+b^2)}).$$

Now, let's assume $N$ is the intersection of the line connecting $C$ and $N_c$ and the line $A$ and $N_a$. So, $N$ is the intersection of the two lines below:

$$y=(\frac{ab-1}{a-b})x+1, \\y=\frac{(a^2-1)(ab-1)}{3a^2b+a^3+b-a}(x+b).$$

Therefore, $N$ is (I calculated this part with WolframAlpha):

$$(\frac{a^3b^2-a^3-a^2b^3-3a^2b+3ab^2+a+b^3-b}{4ab(ab-1)}, \frac{a^2b^2-a^2-b^2+1}{4ab}).$$

To prove the main statement, we just need to show that $N$, $N_b$, and $B$ are colinear. To do so, Wolframalpha says the slope of the line passing through $N$ and $B$ is:

$$\frac{(1-b^2)(ab-1)}{3ab^2+a+b^3-b},$$

which is equal to the slope of the line passing through $B$ and $N_b$ (this is a simple check by hand).

We are done.

Answer 2

The statement is exactly the one in https://mathworld.wolfram.com/PrasolovPoint.html - in OP notations, the ortic triangle is $\Delta H_aH_bH_c$, and its reflection in the nine-point circle is $\Delta N_aN_bN_c$.

For a structural proof, the simplest way to go is to compute points using barycentric coordinates. This is not only showing the required property, but also computes the barycentric coordinates of the point of concurrence in question, from the formula we can see its complexity, recover the result claimed in ETC, and further exhibit interesting other properties - like seeing it is on the line $X(5)X(6)$. I am giving the human solution, complemented for the calculus with computer algebra assistance, easy digestible code, which may be useful for some readers (in this and similar situations).

---

Let $a,b,c$ be the lengths of the sides in $\Delta ABC$. A point $P$ has normed barycentric coordinates $(x,y,z)$ if $P=xA+yB+zC$, with the norming condition $1=x+y+z$. (The relation can be considered using affixes, or vectorially for some / any chosen origin point $\Omega$ in the affine plane so that the vectors relation holds $\Omega P=x\;\Omega A +y\; \Omega B + z\;\Omega C$.) Sometimes it is better to use "projective" coordinates $[x:y:z]$ instead, with $x+y+z\ne 0$, and we pass to the corresponding normed coordinates by dividing by the sum $s=x+y+z$. We often write $\frac 1s(x,y,z)$ instead of $(x/s,\ y/s,\ z/s)$ for this normed version.

Let $S$ being the area of $\Delta ABC$, so $S^2 =s(s-a)(s-b)(s-c)$. The barycentric coordinates of the nine-point center $X(5)$ are $[f(a,b,c)\ :\ f(b,c,a)\ :\ f(c,a,b)]$, see ETC, where $$ f(a,b,c)=a^2(b^2 + c^2) - (b^2 -c^2)^2\ . $$ The norming factor for this representation of $X(5)$ is $$ \begin{aligned} &\sum f(a,b,c):=f(a,b,c) + f(b,c,a)+f(c,a,b) \\ &\qquad =\sum a^2(b^2 + c^2) - (b^2 -c^2)^2 =\sum a^2b^2 + a^2c^2 + 2b^2 c^2 - b^4 - c^4 \\ &\qquad=4a^2b^2 + 4b^2c^2 + 4 c^2 a^2 - 2a^4 - 2b^4 - 2c^4 \\ &\qquad=2(a+b+c)(-a+b+c)(a-b+c)(a+b-c)=32s(s-a)(s-b)(s-c) \\ &\qquad=32S^2\ . \end{aligned} $$

---

Our aim is to show explicitly:

Proposition: There exists an intersection point $X(68)=AN_a\cap BN_b\cap CN_c$, and its barycentric coordinates are $$ \bbox[yellow]{\qquad X(68)= [ \ g(a,b,c)\ :\ g(b,c,a)\ :\ g(c,a,b)\ ] \qquad} $$ with $$ \bbox[yellow]{\qquad g(a,b,c) = \frac{-a^2+b^2+c^2}{a^4 + b^4 + c^4 - 2a^2(b^2+c^2))}\ . \qquad} $$

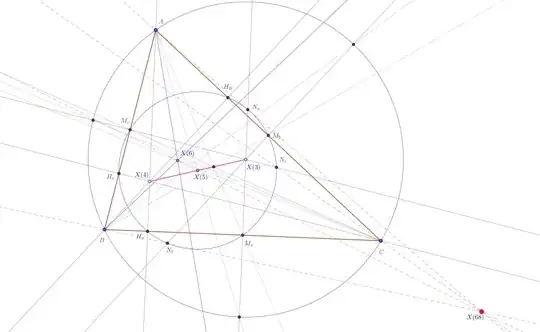
Bonus: The point $X(68)$ also lies on $X(5)X(6)$, the line through the nine-point center $X(5)$, and the symmedian point $X(6)=[a^2:b^2:c^2]$.

Proof: We compute: $$ \begin{aligned} A &= (1,0,0)\ ,\\[2mm] \frac{H_aC}{BC} &=\frac 1a\cdot b\cos C=\frac 1a\cdot b\cdot \frac{a^2 + b^2 -c^2}{2ab} =\frac 1{2a^2}(a^2+b^2-c^2)\ ,\\ H_a&=\left(0,\frac{H_aC}{BC},\frac{BH_a}{BC}\right)= \frac 1{2a^2}(0,\ a^2 + b^2 -c^2,\ a^2 - b^2 + c^2)\ , \\[2mm] X(5) &= (\ x_{X(5)},\ y_{X(5)},\ z_{X(5)}\ )\\ &= \phantom{\frac 1{8S^2}} [\ a^2(b^2+c^2) - (b^2-c^2)^2\ :\ b^2(a^2+c^2) - (a^2-c^2)^2\ :\ c^2(a^2+b^2) - (a^2-b^2)^2\ ]\ ,\\ &= \frac 1{32S^2}(\ a^2(b^2+c^2) - (b^2-c^2)^2\ ,\ b^2(a^2+c^2) - (a^2-c^2)^2\ ,\ c^2(a^2+b^2) - (a^2-b^2)^2\ )\ , \\[2mm] N_a &= 2X(5)-H_a=(\ x_{Na},\ y_{Na},\ z_{Na}\ )\ , \\[2mm] y_{Na} &=2\cdot \frac 1{32S^2}\cdot(b^2(a^2+c^2) - (a^2-c^2)^2) -\frac 1{2a^2}\cdot (a^2 + b^2 -c^2) \\ &=\frac 1{32a^2S^2}\Big(\ 2a^2b^2(a^2+c^2)-2a^2(a^2-c^2)^2 - 16S^2(a^2 + b^2 -c^2)\ \Big)\ . \\[2mm] 32a^2S^2\; y_{Na} &=2a^2b^2(a^2+c^2)-2a^2(a^2-c^2)^2 - 16S^2(a^2 + b^2 -c^2) \\ &=2a^2b^2(a^2-b^2+c^2)+2a^2 b^4-2a^2(a^2-c^2)^2 - 16S^2(a^2 + b^2 -c^2) \\ &=2a^2b^2(a^2-b^2+c^2) + 2a^2 (a^2 + b^2 -c^2)(-a^2+b^2+c^2) - 16S^2(-a^2 + b^2 -c^2) - 32a^2S^2 \\ &=(a^2-b^2+c^2)(2a^2b^2 +16S^2) + 2a^2 (a^2 + b^2 -c^2)(-a^2+b^2+c^2) - 32a^2S^2 \\[2mm] &\qquad (a^2 + b^2 -c^2)(-a^2+b^2+c^2) - 16S^2 \\ &\qquad\qquad=(b^4 - a^4 - c^4 + 2a^2c^2) - (-a^4-b^4-c^4+2a^2b^2+2b^2c^2+2c^2a^2) \\ &\qquad\qquad=-2b^2(a^2-b^2+c^2)\ , \\[2mm] 32a^2S^2\; y_{Na} &=(a^2-b^2+c^2)(2a^2b^2 +16S^2)-4a^2b^2(a^2-b^2+c^2) \\ &=(a^2-b^2+c^2)(-2a^2b^2+16S^2) \\ &=(a^2-b^2+c^2)(-a^4-b^4-c^4+2a^2c^2+2b^2c^2)\ . \\ 32a^2S^2\; z_{Na} &=(a^2+b^2-c^2)(-a^4-b^4-c^4+2a^2b^2+2b^2c^2)\text{ similarly .} \end{aligned} $$ The line $AN_a$ has the equation in barycentric coordinates for a point $P=(x,y,z)$ given by assembly of the coordinates for $A,N_a$, and $P$ in matrix format, than building the determinant: $$ 0= \begin{vmatrix} 1 & 0 & 0\\ x_{N_a} & y_{Na} & z_{N_a}\\ x & y & z \end{vmatrix}\ , $$ so the equation involves only $y,z$ with constant proportionality: $$ \begin{aligned} \frac yz &= \frac{y_{Na}}{z_{Na}} = \frac {(a^2-b^2+c^2)(-a^4-b^4-c^4+2a^2c^2+2b^2c^2)} {(a^2+b^2-c^2)(-a^4-b^4-c^4+2a^2b^2+2b^2c^2)} \\ &= \frac {(a^2-b^2+c^2):(-a^4-b^4-c^4+2a^2b^2+2b^2c^2)} {(a^2+b^2-c^2):(-a^4-b^4-c^4+2a^2c^2+2b^2c^2)} \\ &=\frac{g(b,c,a)}{g(c,a,b)} \ . \end{aligned} $$ Similar equations are written for $BN_b$, and $CN_c$, and the proof is finished by observing that the point $X(68)$ from the proposition satisfies the above equation of $AN_a$, $y:z=g(b,c,a):g(c,a,b)$, as by symmetriy it also the case for $BN_b$, and $CN_c$.

$\square$

---

Sage code:

var('a,b,c');
Ha = 1/2/a^2 * vector([0, a^2 + b^2 - c^2, a^2 - b^2 + c^2])
f(a, b, c) = a^2(b^2 + c^2) - (b^2 - c^2)^2
X5 = vector([f(a, b, c), f(b, c, a), f(c, a, b)])
X5 = 1/sum(X5)  X5    # thus norming it
Na = 2*X5 - Ha
xNa, yNa, zNa = Na

Then:

print(factor(yNa / zNa))

delivers immediately the result of our longer computation:

 (a^4 + b^4 - 2*a^2*c^2 - 2*b^2*c^2 + c^4)*(a^2 - b^2 + c^2)
/
((a^4 - 2*a^2*b^2 + b^4 - 2*b^2*c^2 + c^4)*(a^2 + b^2 - c^2))

(Result was manually rearranged to fit in the MSE line.)

---

We can now also show the bonus point, by computing the determinant: with lines proportional to the barycentric coordinates of respectively $X(6)$, $X(5)$, and $X(68)$, and showing it vanishes: $$ \begin{vmatrix} a^2 & b^2 & c^2\\ f(a,b,c) & f(b,c,a) & f(c,a,b)\\ g(a,b,c) & g(b,c,a) & g(c,a,b) \end{vmatrix} $$

g(a,b,c) = (-a^2 + b^2 + c^2) / (a^4 + b^4 + c^4 - 2*a^2*(b^2 + c^2))
matrix([ [a^2, b^2, c^2],
         [f(a, b, c), f(b, c, a), f(c, a, b)],
         [g(a, b, c), g(b, c, a), g(c, a, b)], ]).det().simplify_full()

And the code delivers rapidly the zero.