Solution explanation for finding the value of Angle $\theta$.

Asked Apr 13 '23 at 23:55

Active Apr 14 '23 at 01:41

Viewed 41 times

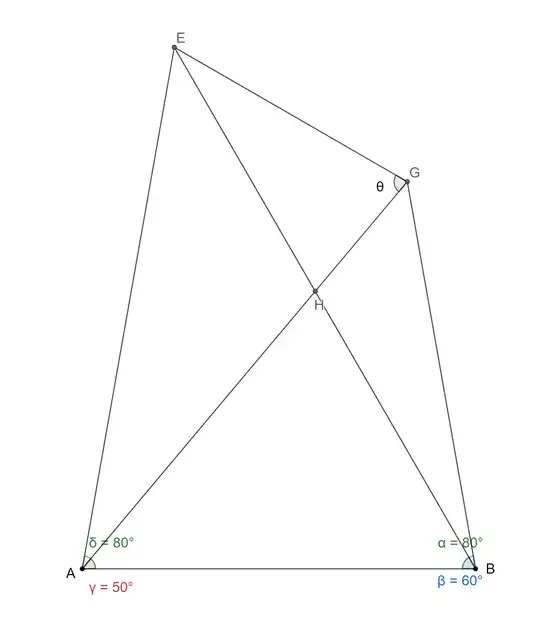
Given the quadrilateral $ABGE$, angles $ABG$ and $EAB$ are both $80$ $degrees$, angle $GAB$ is $50$ $degrees$, and angle $EBA$ is $60$ $degrees$. Find the value of angle $\theta$.

I use the solution found in this link: How to find missing angles in a quadrilateral

Use sine theorem for $ΔABG$ and $ΔAGE$:

$\frac{AB}{\sin{40}}=\frac{AG}{\sin{80}}$

$\frac{AE}{\sin{AGE}}=\frac{AG}{\sin{(20+AGE)}}$

Noting $AB=AE$, we can find $mAGD=30$,$mBEG=80$.

How does $\frac{AE}{\sin{AGE}}=\frac{AG}{\sin{(20+AGE)}}$?

edited Apr 14 '23 at 01:41

asked Apr 13 '23 at 23:55

PRD

1

Related to the original problem of the 80-80-20 triangle. – peterwhy Apr 14 '23 at 00:12
1

Related to Langley's Adventitious Angles. – peterwhy Apr 14 '23 at 00:17
Does this answer your question? How to find missing angles in a quadrilateral - found using a site search. – John Omielan Apr 14 '23 at 00:25
In you update, which solution are you referring to? Where is $D$? – peterwhy Apr 14 '23 at 01:35
@peterwhy, thanks for the feedback, it's $E$. – PRD Apr 14 '23 at 01:41
1

That answer says to use the sine theorem for $\triangle BEG$ to get$$\frac{BG}{\sin BEG} = \frac{BE}{\sin(20+BEG)}.$$ – peterwhy Apr 14 '23 at 02:27

Solution explanation for finding the value of Angle $\theta$.

0 Answers0