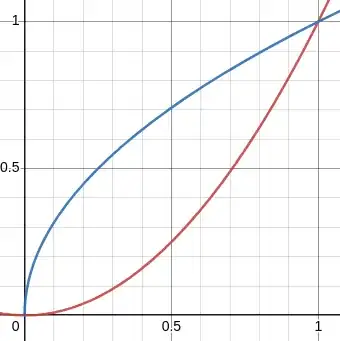
When I scatched the area, I expected the volume obtained by rotating about $y=1$ to be identical with the volume obtained by rotating about the $x$-axis.
To my surprise, calculation shows different results. According my calculation,
volume with rotaing about $y=1$, $\frac{11}{30} \pi$,
volume with rotating about $x$-axis, $\frac{3}{10}\pi$
Are these two volumes are supposed to be different from each other? By looking at the
area, volumes look the same.
- 67,568
- 43
- 308
- 617
- 165
-
2Check this out- https://math.stackexchange.com/questions/3334922/why-the-rotation-of-two-equal-surfaces-with-different-shape-do-not-give-the-sa – Souparna Apr 10 '23 at 04:18
1 Answers
I haven't checked your calculations (and I suppose the volumes might actually be the same, if you simply made an error). But you say:
By looking at the area, volumes look the same.
and I think this is not the case:
The region is clearly fatter at the bottom side ($y$ closer to $0$) than the top ($y$ closer to $1$). Which end would you rather be poked with? The $y=0$ end, surely?
When the region revolves around the line $y=1$, the fat part travels farther than the narrow part, so contributes more to the total volume. You can think of it like this:
Volume = (fat part × travels a long distance) + (narrow part × travels a short distance)
The first factor is a product of two larger numbers and the second is the product of two smaller numbers.
When the region revolves around the line $y=0$, the corresponding formula is
Volume = (fat part × travels a short distance) + (narrow part × travels a long distance)
Now each of the two factors is a product of one larger and one smaller number. This is always less than the other formula.
(If you're not familiar with this, imagine your archery team has member $A$ who is a good shot and $B$ who is not so good. A competition has two events, one worth more points and one worth fewer. You can send one archer to each event. Whom do you send to the event that is worth more points? Alternatively, just consider the example of $10·10+1·1 > 10·1+10·1$.)
So naïvely, without any calculation, I would guess that the solid of revolution around $y=1$ would have a larger volume, as your calculations said.
- 67,568
- 43
- 308
- 617