6

I know that the Mandelbrot set is connected, but what about its interior? It doesn't seem intuitively like it should be, but I can't find any information online confirming this. I can think of an intuitive argument for why the interior shouldn't be path-connected (moving for example from the main cardioid to one of the bulbs, a bifurcation must occur, so any path must cross the boundary) but a) this is completely unrigorous (it's an open problem whether every internal point is in a hyperbolic component, and this argument only works for hyperbolic components - what happens if there are infinitely many non-hyperbolic components?) and b) not being path-connected doesn't imply it's not connected. Can someone point me to some sources which discuss this at all?

Paul Frost
  • 87,968
Ali
  • 130
  • 5
    No. The largest connected component is the interior of the cardioid you see in the picture. If memory serves, such discussion is in Chaos and Fractals: New Frontiers of Science by Peitgen, Jurgens & Saupe – GEdgar Apr 06 '23 at 11:22

1 Answers1

6

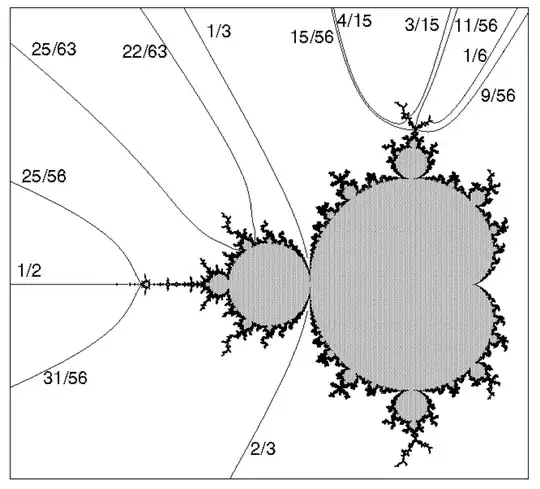
The interior of the Mandelbrot set is definitely not connected. It's rational parameter rays are known to lie in its complement and land at articulation points. This is described in great detail in Rational parameter rays of the Mandelbrot set by Dierk Schleicher. This image, taken from that paper, illustrates some of those rays:

enter image description here

Mark McClure
  • 31,496
  • 1
    So components are connected by one point ( root point) which is boundary point. Am I right ? – Adam Apr 07 '23 at 07:57