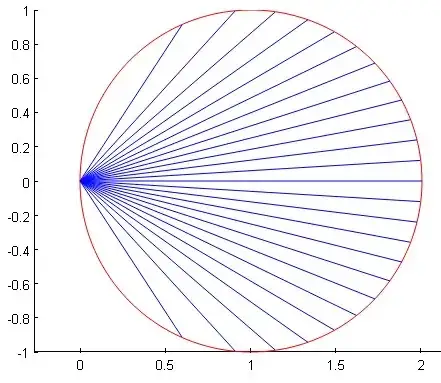
Let us take the common point as the origin. Let $R$ be the radius of the circle, with its origin in $(R,0)$.
The polar equation of this circle is
$$\rho=f(\theta)=2R\cos \theta, \ -\pi/2 < \theta < +\pi/2.$$
The area "browsed" by the radius between $\theta_k$ and $\theta_{k+1}$ (for $1 \le k \le n-1$) is
$$\int_{\theta_k}^{\theta_{k+1}}\frac12 f(\theta)^2 d\theta$$ $$=2R^2\int_{\theta_k}^{\theta_{k+1}}(\cos \theta)^2 d\theta$$
$$=R^2\int_{\theta_k}^{\theta_{k+1}}(1+\cos 2\theta) d\theta$$
$$=R^2 \underbrace{(\theta+\frac12 \sin(2\theta))}_{f(\theta)}]_{\theta_k}^{\theta_{k+1}}$$
$$=R^2\left(f(\theta_{k+1})-f(\theta_k)\right)\tag{1}$$
Therefore, this issue is brought back to the division of line segment $(-\pi/2,\pi/2)$ into $n$ equal parts by function $f$.
If $n$ is the number of "zones", we know that each area is equal to $\frac{\pi R^2}{n}$. Therefore we have to find a sequence of values $\theta_k$ such that :
$$f(\theta_{k+1})-f(\theta_k)=\frac{\pi}{n}\tag{2}$$
$f$ is in fact invertible on $(-\pi/2,\pi/2)$ because $f'(\theta)>0$ on this interval. Therefore, we can write recurrence (2) under the form :
$$\theta_{k+1}=f^{-1}\left(f(\theta_k)+\frac{\pi}{n}\right)\tag{3}$$
This recurrence works because :
we know the initial value $\theta_0=\frac{\pi}{2}$.
though $f^{-1}$ hasn't an analytic expression, its values $\theta=f^{-1}(u)$ can be computed by solving equation $f(\theta)=u$ by definition of an inverse function.
Here is a Matlab implementation (where inverse function $f^{-1}$ is denoted $g$ and computed as a separate function).
function main
clear all;close all;hold on;axis equal;
u=0:pi/100:2*pi;plot(1+cos(u),sin(u),'r');
n=26;
f=@(t)(t+0.5*sin(2*t));
t=-pi/2; % \theta_0
for k=1:n-1
t=g(f(t)+pi/n); % implem. of formula (3)
plot([0,1+cos(2*t)],[0,sin(2*t)]);
end;
function t=g(u);
syms t1
X=solve(t1+0.5*sin(2*t1)==u);
t=X(1);
Remark : In fact, this answer can be considered as "issued" from the answer I had given here to a completely similar question. The formulation of this answer wasn't direct enough (this explains maybe why it hadn't been upvoted) ; I think the present version, with its accompanying program, is clearer.
