1

I have a nonlinear first-order recurrence of the form $$ a_n=a_{n-1}+\sqrt{a_{n-1}}, $$ with $a_1=b>0$. While simple in form, I suspect there is no closed-form due to the nonlinear square root term. However, the asymptotics of the recursion are of interest to me.

Playing around with different values of $b$ I (apparently) discovered for large $n$ $$ a_n\sim Cn^2. $$ But why is this?

Larger values of $b$ ($b\geq 1$) show quicker convergence to the quadratic form as compared to $b<1$.

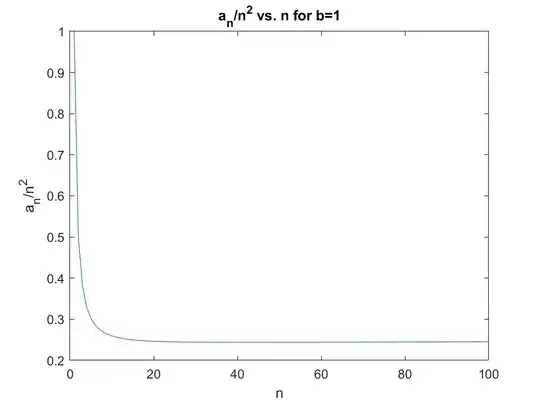
Here is a plot of $a_n/n^2$ vs. $n$ for $b=1$: enter image description here

Also, here is a table of the first several $a_n$ when $b=1$:

$$ \left( \begin{array}{cc} n & a_n\\ 1 & 1 \\ 2 & 2 \\ 3 & 2+\sqrt{2} \\ 4 & 2+\sqrt{2}+\sqrt{2+\sqrt{2}} \\ 5 & 2+\sqrt{2}+\sqrt{2+\sqrt{2}}+\sqrt{2+\sqrt{2}+\sqrt{2+\sqrt{2} }} \\ \end{array} \right) $$

Aaron Hendrickson
  • 6,388
  • 4
    Check this: https://math.stackexchange.com/q/1196979/42969 – Martin R Mar 27 '23 at 14:17
  • Heuristically, $a_n-a_{n-1}=\frac{da_{n-1}}{dn}\cdot1+\frac12\frac{d^2a_{n-1}}{dn^2}\cdot1+...=\sqrt {a_{n-1}}$. Supposing that at $n\to\infty\quad\frac{da_{n-1}}{dn}\gg\frac{d^2a_{n-1}}{dn^2}\gg...\quad\Rightarrow\quad\frac{da_{n-1}}{dn}\approx\sqrt {a_{n-1}},\Rightarrow,a_{n-1}=\frac14n^2+o(n^2)$. The condition $\frac{da_{n-1}}{dn}\gg\frac{d^2a_{n-1}}{dn^2}$ is met. – Svyatoslav Mar 27 '23 at 14:19
  • It seems that $,a_{n-1}=\frac{n^2}2-\frac{n\ln n}{4}+Cn+o(n);,n\gg1,$, where the constant $C$ depends on $a_1$ – Svyatoslav Mar 27 '23 at 14:57
  • @Svyatoslav How did you come to that result? – Aaron Hendrickson Mar 27 '23 at 15:08
  • 1
    Sorry, corrected a typo: should be $,a_{n-1}=\frac{n^2}{\color{red}{4}}-\frac{n\ln n}{4}+Cn+o(n);,n\gg1,$, where the constant $C$ depends on $a_1$. Step by step iterations: $a_{n-1}=a^0_{n-1}+a^1_{n-1}+...$, where (we suppose) $a^0_{n-1}\gg a^1_{n-1}\gg...$. Then we get $\frac{d(a^0_{n-1}+a^1_{n-1})}{dn}+\frac12\frac{d^2a^0_{n-1}}{dn^2}\approx\sqrt{a^0_{n-1}+a^1_{n-1}}\approx \frac n2+\frac{a^1_{n-1}}n$. Searching for $a^1_{n-1}=bn+cn\ln n,\Rightarrow, c=-\frac14$, and $b$ cannot be found from the equation. – Svyatoslav Mar 27 '23 at 15:28
  • $\frac{a_n-a_{n-1}}{n-(n-1)} = \sqrt{a_{n-1}}$ or $a_n'=\sqrt{a_n}$ or $a_n = 4n^2+C$ – Cesareo Mar 27 '23 at 17:45
  • Does this answer your question? Aproximation of $a_n$ where $a_{n+1}=a_n+\sqrt {a_n}$. My answer is very precise and is for general $a_1>0.$ – Somos Apr 04 '23 at 17:34

0 Answers0