non sequential spaces

Question

I am looking for a space which is not sequential. I tried to build this example: Take $X$ to be a countable union of the folloing points: $X= (\bigcup_{n=1}^\infty( \bigcup_{k=1}^\infty (\frac1n,\frac1k)))\cup(\bigcup_{i=1}^\infty(0,\frac1i))\cup\{(0,0)\} $ ($n,k,i$ are natural numbrs). Define Basis neighborhoods of every point in $X$ to b:

1. if a point is of the form $(\frac1n,\frac1k)$, Then an open basis neighborhood of $x$ will be (the intersection of) vertical open segments containing $(\frac1n,\frac1k)$ (with $X$).

2. if a point is of the form $(\frac1n,0)$, Then an open basis neighborhood of $x$ will be (the intersection of) open discs containing $(\frac1n,0)$ (with $X$).

3. an open basis neighborhood of $(0,0)$ is (the intersetion of) open disc containing $0$ in it's boundary union with $(0,0)$ itself (with $X$).

This is how it looks like:

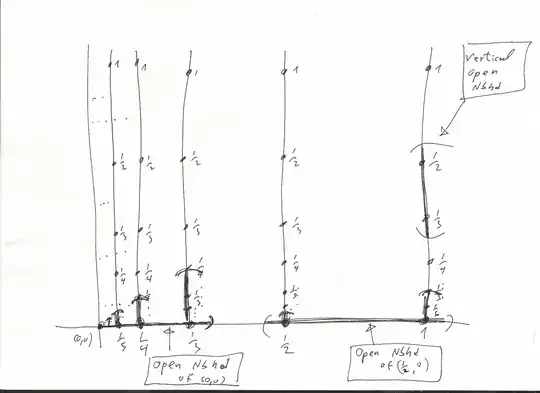
I think that this is a topology and that $(X,T)$ is not sequential since take a subset $A$ of $X$ which is $A= (\bigcup_{n=1}^\infty( \bigcup_{k=1}^\infty (\frac1n,\frac1k)))$.

Then $(0,0)$ is contained in $\overline{A}$ but there is no sequence in $A$ which is converges to $(0,0)$, (because if non of the points are on $X-axis$, I can always find an open neighborhood of $(0,0)$ not containing it) What do you think, am I right?

Thank you!! Shir

Answer 1

I don't quite understand the topology you're describing. Are you just giving your set the subspace topology as a subset of $\mathbb{R}^2$? If so, I don't think your example works because the sequence $(\frac{1}{n},\frac{1}{n})$ is in $A$ and converges to $(0,0)$.

Here is an example of a nonsequential space. Let $X$ be an uncountable set and let $\mathcal{T}$ be the topology given by the empty set along with subsets of $X$ whose complement is countable. This is often called the cocountable topology.

To see that this set is not sequential, suppose that $x_n$ is a convergent sequence in $X$, and let $x$ be the limit point. Consider the countable set of points $x_n$ that are not equal to $x$ and let $U$ be the complement of this set. Since $U$ contains $x$, there must be some $N$ such that $x_n\in U$ for all $n\ge N$. This implies that $x_n=x$ for all $n\ge N$. It follows that every subset of $X$ is sequentially open, but not every subset of $X$ is open.

Answer 2

As I understand $(X,T)$, $X$ is the set $$\bigcup\limits_{n,k \geq 1} \left\{ ( x,y) \mid x= \frac{1}{n} \ \text{or} \ 0, \ y= \frac{1}{k} \ \text{or} \ 0 \right\},$$

and $T$ is the topology generated by $$\{(x,y) \in X \mid (x,y) \neq 0\} \cup \bigcup S,$$

where $S$ is the set of all subsets of the form $$ \left\{ \left( \frac{1}{n}, \frac{1}{k_n} \right) \mid m \leq n \leq + \infty, \ m_n \leq k_n \leq + \infty\right\}.$$

I agree that $(0,0)$ is in the closure of $A=X \cap (0,+ \infty)^2$ but not in the sequential closure of $A$:

Suppose that $ \left( \left( \frac{1}{n_i}, \frac{1}{k_i} \right) \right)$ converges to $(0,0)$. Without loss of generality, we may suppose that $(1/n_i)$ is an decreasing sequence converging to $0$ as $i \to + \infty$. Let $p_i>n_i$ for all $i$. Then the above sequence does not meet the open neighborhood

$$\left\{ \left( \frac{1}{n}, \frac{1}{k_n} \right) \mid m \leq n \leq + \infty, \ m_n \leq k_n \leq + \infty\right\},$$

where $m_n=p_i$ if $n=n_i$ and $1$ otherwise.

---

Another example of non-sequential space is Arens-Fort space $X$. Because singletons are clopen, every convergent sequence is eventually constant, so any subset is sequentially open whereas $X$ is not discrete.

An interesting fact is that $X$ is still countably generated. Many properties of $X$ can be found here.

Answer 3

I have continued thinking about this example with respect to notions of sequential, Frechet Urysohn, and Countable generation. Wouldn't it be more correct that The space described above is sequential but not Frechet Urysohn? Because, if I get it correctly, Sequentiality does allow itterations of limits while Frechet Urysohn does not. And, as I understand it, every point of the form $(\frac1n,0)$ is a limit point of $A$, and $(0,0)$ is a limit point of the sequence $\{(\frac1n,0)\}$ What do you think? Thanks! Shir