4

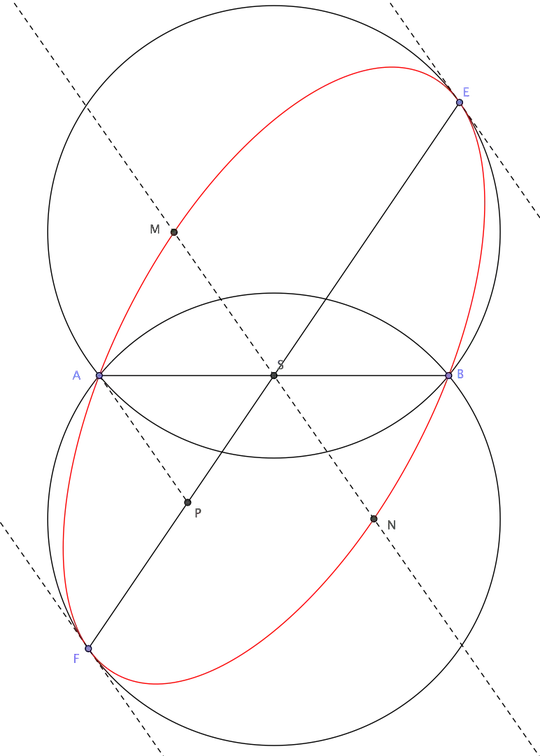
enter image description hereLet two circles $C$ and $C’$ intersecting at points $A$, $B$. I would like to construct an ellipse passing through $A$ and $B$ using the $5$ points construction of GeoGebra (foci unknown). The problem is that the ellipse must have two points of tangency ($E$ with $C$ and $F$ with $C’$). Do you know a method that uses inversion ? Is there a way to impose this tangency ? Many thanks to any hint/help.

Jean Marie
  • 88,997
3809525720
  • 407
  • 1
    To be clear: should the ellipse have one tangency for each circle, or should the ellipse be have two points of tangency for each circle? Also, a diagram of what an example would look like would help. – Semiclassical Mar 08 '23 at 18:19
  • The ellipse won't be unique. Do you want any ellipse satisfying that? Or do you have another condition in mind? – jjagmath Mar 08 '23 at 18:20
  • Semiclassical: one tangency for each circle. – 3809525720 Mar 08 '23 at 18:21
  • Jjagmath: any ellipse should fit. – 3809525720 Mar 08 '23 at 18:22
  • Semi classical: you’re right. I edited my post with a picture – 3809525720 Mar 08 '23 at 18:29
  • It's a good diagram, but you may want to modify the text of the problem to match. (Circles $C,C'$, tangent to the ellipse at points $E,F$ respectively.) – Semiclassical Mar 08 '23 at 18:31
  • To approximate such an ellipse with Geogebra isn't too bad: Pick two points $E,E'$ on $C$ and a point $F$ on $C'$, then construct an ellipse passing through $ABEE'F$. Now move point $E'$ so it coincides with $E$ to create the first tangency, then move $F$ until it's also a point of tangency. (Note that this depends on the choice of $E$ and hence is not unique.) – Semiclassical Mar 08 '23 at 18:34
  • Yes but I’m looking for a way to designate the five points to GeoGebra and then, he draws me the ellipse passing through them. – 3809525720 Mar 08 '23 at 18:38
  • One thing to notice: tangents at points $E$ and $F$ should be parallel ! – 3809525720 Mar 08 '23 at 18:51
  • If the tangents at E and F are parallel, and the circles are congruent, then all you have is a point A and E and the tangent at E, the other information is redundant, it does not add anything. –  Mar 08 '23 at 19:11
  • I doubt there is a solution using inversion : in the best case, the inverse of an ellipse is a limaçon, not a very simple curve... – Jean Marie Mar 17 '23 at 21:12
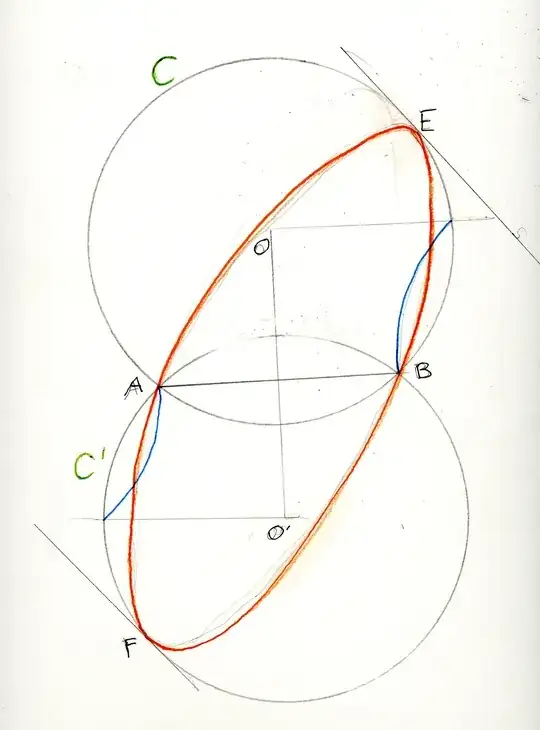
  • Is anything wrong with my construction? I uploaded it to GeoGebra for you to understand it better: https://www.geogebra.org/m/dss3bjng – Intelligenti pauca Mar 17 '23 at 21:42

2 Answers2

5

I'm assuming the circles to be congruent, otherwise the problem has no solution, in general. Point $E$ can then be chosen at will, while $F$ is the reflection of $E$ about the midpoint $S$ of $AB$, which is also the center of the ellipse.

Draw the line $t$ tangent to the circle at $E$, then draw through $S$ a line $r$ parallel to $t$ and call $M$, $N$ the (unknown) intersections between $r$ and the ellipse. $EF$ and $MN$ are conjugate diameters.

Draw a point $P$ on $EF$ such that $AP\parallel r$. By the properties of conjugate diameters we have then: $$ {AP^2\over SM^2}+{SP^2\over SF^2}=1. $$ From that you can compute $SM$: $$ SM={AP\over\sqrt{1-SP^2/SF^2}} $$ and construct point $M$ on line $r$.

enter image description here

Intelligenti pauca
  • 55,765
  • 1
    {+1] Once more, very well done. It would be interesting to study the arc on the upper circle where $E$ can be chosen in order the tangency condition can be fulfilled (of course it would be necessary for that to know ratio $d/r$ where $d$ is the distance between the centers and $r$ the common radius). – Jean Marie Mar 17 '23 at 21:08
  • @JeanMarie I'm not sure I understand what you mean. Point $E$ can be chosen anywhere on the upper circle. – Intelligenti pauca Mar 17 '23 at 21:13
  • Ah is it so ? Whatever the ratio $d/r$ ? How can we be sure of that ? – Jean Marie Mar 17 '23 at 21:18
  • @JeanMarie Why do you think the construction could fail for some choice of $E$? The properties of conjugate diameters ensure that the parallel to $MN$ through $E$ is tangent to the ellipse. – Intelligenti pauca Mar 17 '23 at 21:22
  • You are right... – Jean Marie Mar 17 '23 at 21:30
  • @JeanMarie I uploaded the construction to GeoGebra: https://www.geogebra.org/m/dss3bjng – Intelligenti pauca Mar 17 '23 at 21:31
  • Thank you : indeed nothing prevents $E$ to be anywhere on the outer arc $AB$... – Jean Marie Mar 17 '23 at 21:35
  • Thank you for those who answered. I was helped for the following partial solution that gives the two points of tangency with circles $C’$ and $C$. But it doesn’t work with GeoGebra because it still misses the 5th point. Choose any point F on the circle C’. Then draw the tangent at F to C’. Draw the diameter (EE’) (of the second circle C) that is orthogonal to the tangent at F to C’. Tangents to C at E and E’ are parallel with tangent to C’ at F. Lines (FE) and (FE’) are passing through the homothetic centers of circles C and C’. The ellipse is then tangent to C at E and to C’ at F. – 3809525720 Mar 17 '23 at 23:32
  • Your analytical solutions are interesting but I was looking for a more synthetic solution using geometric transformations stored in the GeoGebra menu. I don’t think there is any ! – 3809525720 Mar 17 '23 at 23:42
  • @3809525720 My solution is not "analytical": the formula for $SM$ can be easily turned into a geometric construction, if that is what you want. And the other equation was introduced by Apollonius of Perga in 3rd century BC. – Intelligenti pauca Mar 18 '23 at 16:33
  • @3809525720 On the other hand, to find the fifth point by using only a geometrical transformation is clearly impossible, as several people pointed out in the comments. – Intelligenti pauca Mar 18 '23 at 16:39
2

Assuming the two circles are congruent, and that the tangents at $E$ and $F$ are parallel, then from symmetry, we know that the center of the ellipse is at the midpoint of $A$ and $B$. Let this point be $M_{AB}$, i.e.

$ M_{AB} = \dfrac{1}{2} (A + B ) = (x_1, y_1) $

In addition to the center $M_{AB}$ we know that point $A$ is on the ellipse. And we also have point $E$, and finally we know the slope of the tangent at point $E$. The equation of the ellipse satisfying these conditions can be derived from the equation of an ellipse centered at $M_{AB}$.

$ (r - M_{AB})^T Q (r - M_{AB} ) = 1 $

where $ r = [x, y]^T $ and $Q = \begin{bmatrix} a && b \\ b && c \end{bmatrix}$

Expanding,

$ a x^2 + 2 b x y + c y^2 - 2 a x x_1 - 2 b ( x y_1 + y x_1) -2 c y y_1 + a x_1^2 + 2 b x_1 y_1 + c y_1^2 -1 = 0 $

Which is nice and linear in the $3$ unknowns: $a,b$, and $c$.

Using the coordinates of $A$ and $E$ gives two independent equations in the three unknowns.

Next, differentiate the above equation implicitly with respect to x, this will give

$ 2 a x + 2 b (x y' + y ) + 2 c y y' - 2 a x_1 - 2 b (y_1 + y' x_1) -2 c y' y_1 = 0 $

Substitute point $E$ and the slope at point $E$ into this equation, which provides the third independent equation.

Solve the system of $3$ equations in the $3$ unknowns, and this gives the values of $a,b$ and $c$.

Having obtained $a,b,c$, you now have the equation of the ellipse, which you can feed to Geogebra to obtain a plot.