How can I decide if this regular graph is toroidal?

Question

I am considering the following graph $G$ with $10$ vertices and $30$ edges:

• Vertices of $G$ are the ten two-element subsets of $\{A,B,C,D,E\}$
• Vertices $u$ and $v$ are adjacent if $$|v\cap u| = 1.$$

So for example the vertex $AB$ is adjacent to $AC, AD, AE$ and to $BC, BD, BE$.

It is plausible that this graph could be embedded on a torus. If it were, we might expect the embedding to have $20$ triangular faces, because there are $30$ edges and each edge would be part of two of the faces. One such face would contain the three vertices $AB, AC,$ and $ BC$ and their three edges. Then we would have $F-E+V=0$ as required.

I have not been able to construct such an embedding and I suspect that it is not possible. For example, the attempt below starts well but is blocked because the embedding of edge $CD-CE$ has nowhere to go; the straight path is blocked by the embedding of $AC-BC$.

But I don't know how to proceed from here, either to produce a proof that there is no embedding, or an actual embedding.

Does anyone have suggestions?

Answer 1

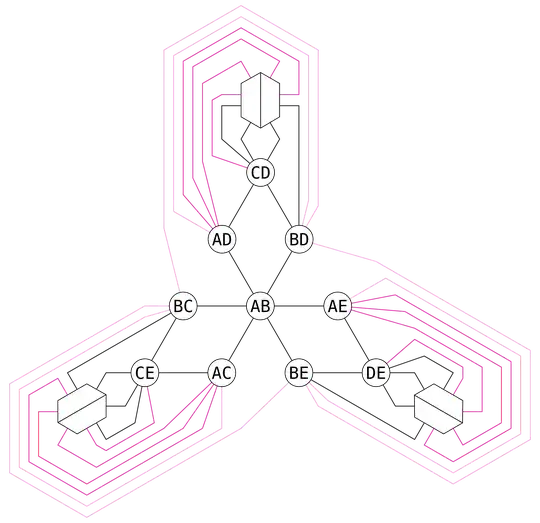
This graph is the complement of the Petersen graph and the Johnson graph $J(5,2)$. A House of Graphs search reveals that its graph genus is $2$, so a toroidal embedding is not possible.

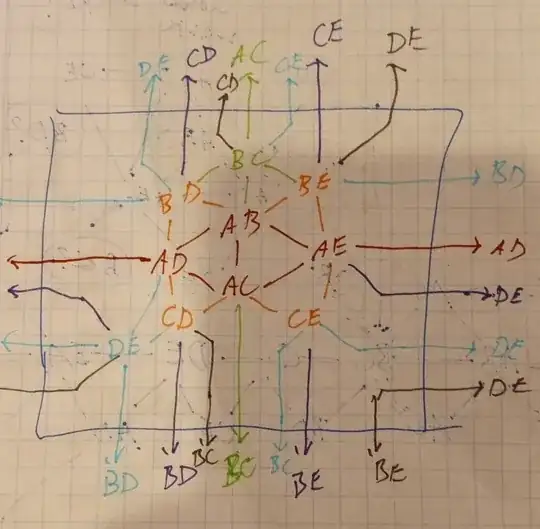
An independent proof of non-toroidality can fairly easily be done with a quick computer search. Consider the following subdivision of $K_{3,3}$ in the graph:

From “A Faster Algorithm for Torus Embedding” (Woodcock, Jennifer Roselynn; University of Victoria M.S. Thesis 2006) there are $20$ non-isomorphic ways to embed the $K_{3,3}$ subdivision on the torus, not ignoring labels (p.24). It remains to check that for every embedding the remaining edges cannot be added without making a crossing.

While $J(5,2)$ is not toroidal, you have shown that removing any edge (for the graph is symmetric) makes it toroidal, so $J(5,2)$ forms a minimal topological obstruction to toroidality.

---

A much slicker way to show that $J(5,2)$ is non-toroidal is to note, as you have done, that any toroidal embedding would triangulate the torus. The orientable combinatorial embedding (see pp. 7, 8 of Woodcock) of such a triangulation satisfies Ringel's Rule R* (cf. Jungerman):

If $vwx$ appears in the (cyclically ordered) neighbour list for $u$, $xuv$ appears in the neighbour list for $w$.

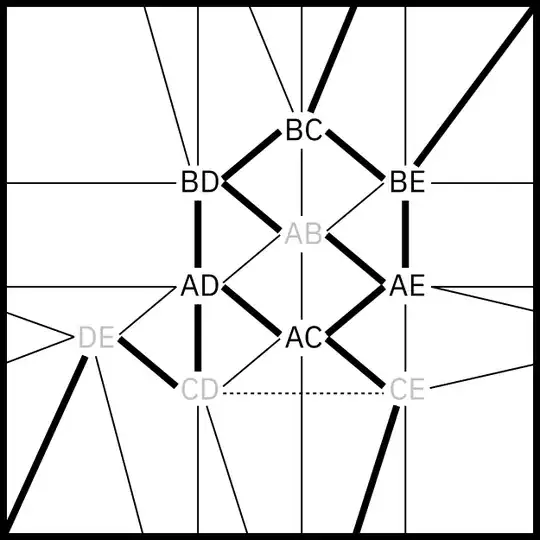
Now the graph induced by the neighbours of any vertex $v$ is a triangular prism, and $v$'s neighbour list must read as a Hamiltonian cycle for this prism (otherwise $v$ would not be surrounded by triangles). The prism has $6$ Hamiltonian cycles up to cyclic rotation, but all are equivalent under the whole graph's symmetries, so if we show that one such cycle does not lead to an embedding we immediately prove non-toroidality.

Suppose $AB$'s neighbour list is $(AC,BC,BD,BE,AE,AD)$. This forces by one application of Rule R* the neighbour lists of two of the six neighbours as $$AC\to(AB,AD,AE,CE,CD,BC)$$ $$AD\to(AB,AE,DE,BD,CD,AC)$$ Since $AC$ has $(AB,AD,AE)$ in its list, Rule R* says that $AD$ must have $(AE,AC,AB)$ in its list, but it does not. Thus no embedding is possible and $J(5,2)$ is non-toroidal.

---

Here is an embedding of $J(5,2)$ on the double torus. The three hexagons are joined by a Y-shaped handle in the most natural way, which adds only $2$ to the genus and not $3$.