2

With Sarkovskii's theorem I want to conclude the chaotic behavior of the logistic map $f(x)=r \cdot x(1-x)$. I can't find a value of $x$ which leads to a periodic three orbit. Does anyone know a value of $x$ that leads to a periodic three orbit? If I found such starting point of the iteration, I could use Sarkovskii's theorem to argue the chaotic behavior of the logistic map at $r=4$.

The following pictures (generated with Mathematica) show the graphic iterations of the logistic map for different starting points:

Iteration of the logistic map with starting point $x=0.50000$:

Iteration of the logistic map with starting point $x=0.50001$:

Alp Uzman
  • 12,209
David
  • 77
  • I know Li and Yorke wrote a paper titled "Period three implies chaos", but in the years since that paper was published a definition of "chaos" has come to be accepted which differs from the one Li and Yorke were using. Proving $f(x)=4x(1-x)$ is chaotic is not so hard, but the proof has nothing to do with period three. – Gerry Myerson Feb 28 '23 at 12:57

2 Answers2

8

It is well-known that a parametrization of $x_n=\sin^2(\pi \theta_n)$ transforms the dynamic to $\theta_{n+1}=2\theta_n\bmod 1$, the destructive left-shift of the binary digit sequence of $\theta_n$, removing the leading digit in every step. For a period-3 cycle you now need a rational number with a period-3 binary digit sequence like $\theta_0=1/7$, thus take $$x_0=\sin^2(\pi/7).$$

This logic also predicts that using double precision floating point numbers the cycle will deteriorate in about 50 iterations, as then the encoding bits of the initial value are used up, and the remaining contents in $x_n$ will be random bits produced by the floating point truncation errors during the computation.

Lutz Lehmann
  • 131,652
  • So is the conclusion correct, that the binary digits e.g. $.000010000100001...$ create an period-$5$ cycle and that we can create with this method a cycle of every period $p \in \mathbb{N}$?

    And can one say that those created cycles of period $p$ are unstable cycles (in particular not attractors of period $p$), because the logistic map has a positive Lyapunov-exponent for $r=4$? But than again, the bifurcation-diagram shows the accumulation points of the iterates of $f$, how can there be accumulation points if the Lyapunov-exponent is positive? Or are these points unstable periodic points?

     – David Mar 06 '23 at 20:25
  • 1
    Yes, $1/31,2/31,4/31,8/31,16/31,32/31=1+1/31$ does form a 5-cycle. // You can not rely on the standard iteration diagram, as the production of new random digits is not really random. This could perhaps be helped by adding a better random noise, small but dominating the floating-point noise. – Lutz Lehmann Mar 06 '23 at 21:45
  • Okay thank you!

    I have just one final question: I created a cobeweb-diagramm of the logistic map for the starting point $x_0=\sin^2\bigl(\frac{\pi}{7}\bigr)$. If I just use $30$ iterations everything seems fine, so that we have a period-$3$ cycle. But if I iterate the map e.g. $300$ times, we don't get a period-$3$ orbit anymore but something aperiodic. Is this simply caused by the finite digit numbers of Mathematica, that we can't really start the iteration at $\sin^2\bigl(\frac{\pi}{7}\bigr)$ but a rational number with finite digits?

     – David Mar 06 '23 at 22:23
  • Yes. For longer sequences that follow the period you need multi-precision types that have more correct digits at the start. – Lutz Lehmann Mar 06 '23 at 23:12
2

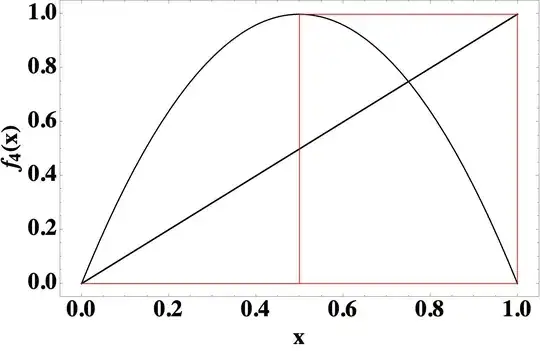
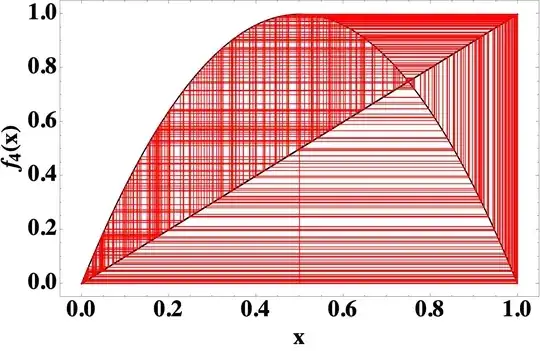
To build up on the Lutz Lehmann's answer, the map $\Phi:\theta\mapsto \sin^2(\pi\theta)$ exhibits the logistic map $L:x\mapsto 4x(1-x)$ as a $2:1$ factor of the doubling map $E: \theta\mapsto 2\theta \mod1$. This latter map has (exactly) $8-2=6$ points of period $3$, hence the logistic map $L$ has at least $3$ points of period $3$, that is, at least one $3$-cycle ($\dagger$). Here is a cobweb diagram exhibiting the cycle given by the semiconjugacy $\Phi$:

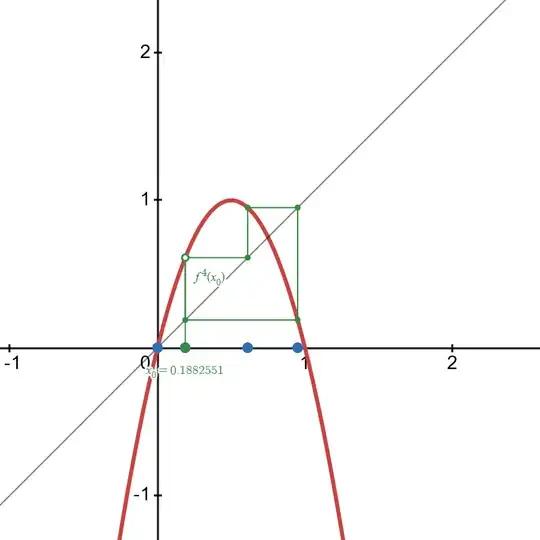
enter image description here

(The interactive graph is available at: https://www.desmos.com/calculator/ucr4tj7zdq)

($\dagger$) In an earlier version of this answer I had claimed that the logistic map $L$ has exactly one $3$-cycle; as David pointed out in a comment this is false. The true statement is that $L$ has exactly two $3$-cycles:

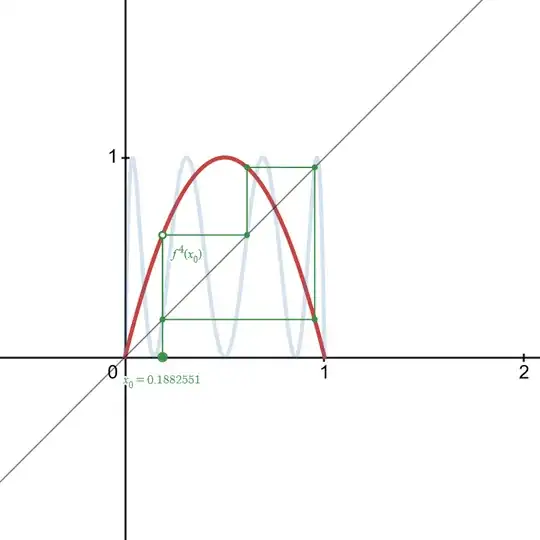
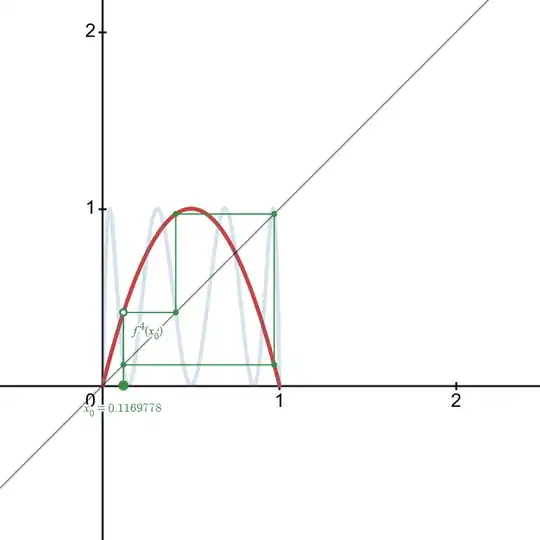
enter image description here

enter image description here

(The first cycle is the one discussed already. The interactive graph is available at: https://www.desmos.com/calculator/mk3qfhibgb)

The error in the previous version of my answer stemmed from assuming that any $3$-periodic point of $L$ must be the image of a $3$-periodic point of the doubling map $E$ under the semiconjugacy $\Phi$. In reality $(\dagger\dagger)$ we have that if $\theta$ is a point with

$$\Phi\circ E(\theta) = \Phi(\theta), \quad\quad(\star)$$

then $\Phi(\theta)$ is a fixed point of $f^3$, and indeed any fixed point of $f^3$ is of the form $\Phi(\theta)$ for such a $\theta$. Expanding $(\star)$, for numerical values of initial conditions for $3$-cycles $\theta$ is required to solve one of the two analytic equations

$$\sum_{n\in\mathbb{Z}_{\geq0}}\dfrac{(-1)^n(8^{2n+1}\pm 1)\pi^{2n+1}}{(2n+1)!}\theta^{2n+1}=0.$$

There are various methods that approximate zeros of analytic equations; but for the sake of this discussion it seems it's sufficient to refer to graphs (of concatenations); indeed the interactive graph at https://www.desmos.com/calculator/mwbq9gpc5d does count the distinct initial conditions for $3$-cycles accurately. (Once the existence of a cycle is established, one can also use the cobweb diagrams to find numerical values.)

$(\dagger\dagger)$ More generally if $X,Y$ are compact metric spaces and $f:X\to X$, $g:Y\to Y$, $\Phi:X\to Y$ are continuous maps with $\Phi$ onto and $\Phi\circ f=g\circ \Phi$, then

$$\{x\in X | \Phi\circ f(x)=\Phi(x)\} = \Phi^{-1}(\text{Fix}(g)).$$

Alp Uzman
  • 12,209
  • Thanks that was exactly what I was looking for! So the stable orbit of period three of the logistic map $x_{n+1}=r \cdot x_n (1-x_n)$ at $r=4$ isn't simply a rational number, but one can also find a orbit of period three for the starting point of the iteration $x_0=sin^2\Bigl(\frac{6}{7} \pi \Bigr)$ – David Mar 02 '23 at 09:20
  • You said that the logistic map has exactly $3$ points of period $3$. But as you said, that the third iterated of the logistic map has $8$ intersections with the bisector, wich represent $8$ fixed points and $6$ points have period $3$, so we have $\frac{6}{3}=2$ orbits of period three. But just one orbit forms an attractor (stable orbit or stable circle of period $3$) and the other orbit is a unstable orbit or unstable cycle of period $3$, but this unstable orbit still has period $3$. – David Mar 06 '23 at 16:25
  • @David Apologies, you are right. I have edited the answer accordingly. Thank you for the correction. – Alp Uzman Mar 13 '23 at 21:25