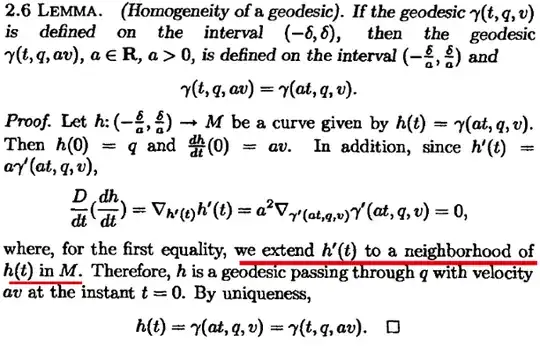0

enter image description here

Definition of covariant derivative of vector fields along a curve

I don't really understand the red line. For sure, to ensure $\frac{D}{d t}\left(\frac{d h}{d t}\right)=\nabla_{h^{\prime}(t)} h^{\prime}(t)$, $h^{\prime}(t)$ should be induced from a vector field $Y \in \mathcal{X}(M)$, i.e., $$h'(t)=Y(h(t)).$$ I think, that is why the $h'(t)$ is extended to a neighborhood of $h(t)$ in $M$. (by bump function, it could be a smooth vector field on $M$.) But how can $h'(t)$ be extended to a neighborhood of $h(t)$ in $M$? Since $h'(t)$ is a vector field along a curve, how could we smoothly extend a field along a curve to an open subset?

gsoldier
  • 185

1 Answers1

1

The question is local, so we can assume that the geodesic $\gamma=\{h(t)\vert t\in(-\varepsilon,\varepsilon)\}$ is an embedded submanifold of $M$. The velocity $h'(t)$ is an element of $T_{h(t)}M$, so we can interpret $h'$ as a section of $TM$ restricted to $\gamma$, and the problem can be generalized as follows: given a vector bundle $E\to M$, restrict it to a submanifold $Z\subset M$, and consider a section $\sigma:Z\to E_{\restriction Z}$. Can we always extend it to a neghbourhood of $Z$?

You should be able to find an answer in these related questions:

Extension of Sections of Restricted Vector Bundles

Proving The Extension Lemma For Vector Fields On Submanifolds

Let me know if you find this helpful, or if you'd like me to provide more details.

Johnny Lemmon
  • 2,332