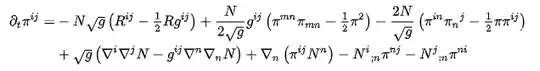What is $\nabla_i \nabla _j N_i$ in differential geometry?

Question

Wading our way into notations used in numerical relativity here , suppose the covariant derivative is defined as

$$ \nabla_j N_i = \frac{dN_i}{dx^j} - \Gamma^k_{ij}N_k $$

with implied summation over k.

What should we compute for the covariant derivative of the covariant derivative:

$$ \nabla_i \nabla _j N_i = ? $$

as in

A vector field is a $(1,0)$ tensor field. The covariant derivative of a $(p,q)$ tensor field is a $(p, q+1)$ tensor field (it adds a contravariant component each time). You thus need to look up the formula for differentiating a tensor field, specifically a $(1,1)$ tensor field. — Brevan Ellefsen, Feb 09 '23 at 03:59
@BrevanEllefsen computationally do you mean we compute $\nabla_j N_i$ for every point on the grid first, and then do a second round of $\nabla$ computation upon this first order numerical field to get at $\nabla \nabla N$? — James, Feb 09 '23 at 04:50
Grid? What?? The calculation is just straightforward via the product rule (in red) and the definition $\nabla_i v = (\partial_iv^j + \Gamma^j_{ik}v^k)e_j$: $$\nabla_i \nabla_j v = \nabla_i((\partial_j v^k+ \Gamma^k_{jl}v^l)e_k)=(\partial_i(\partial_j v^k+ \Gamma^k_{jl}v^l)+(\partial_j v^m+ \Gamma^m_{jl}v^l)\Gamma_{im}^k)e_k,.$$ or in component form (recall $v^k$ is the $k$-th component of $v = v^ke_k$): $$(\nabla_i \nabla_j v)^k=\partial_i \partial_j v^k + \color{red}{v^l \partial_i \Gamma^k_{jl}+\Gamma^k_{jl}\partial_i v^l} + \Gamma_{il}^k \partial_j v^l+ \Gamma^k_{im}\Gamma^{m}_{jl}v^l,.$$ — Brevan Ellefsen, Feb 09 '23 at 05:00
(note the above is for a vector field $v$. For a covector field just replace the sum with subtraction as in your post and proceed) — Brevan Ellefsen, Feb 09 '23 at 05:14
No problem. Note the formula looks very slightly different in index notation, e.g. see here. Be a bit careful in mixing formulas from different sources in case they are using indices differently — Brevan Ellefsen, Feb 09 '23 at 06:09
@BrevanEllefsen thank you once again. If the implementation is right, computing $\frac{d\pi_{ij}}{dt}$ allows us to compute $\frac{dg_{ij}}{dt}$ at every location, which when compared will give the same result as the $g_{ij}$ value written at the $t+dt$ location, right? I am still a bit puzzled by what the program of ADM relativity is, since no new insight is gained, and the full 4-dimensional time evolution must first be stitched/evolved manually into 4-dimensional $g_{\mu\nu}$ data, what exactly do we gain by painstakingly calculating $\frac{d\pi_{ij}}{dt}$ and $\frac{dg_{ij}}{dt}$? — James, Feb 09 '23 at 15:07
I'm afraid I don't know a thing about numerical relativity (and barely anything about relativity in general). You might have more luck asking that on a physics-oriented website. — Brevan Ellefsen, Feb 09 '23 at 18:30

score 3 · Answer 1 · answered Feb 09 '23 at 05:17

The wiki page on Covariant derivative has a complete list with explanations, which I summarise here.

To take the covariant derivative of a tensor field $T$ of type $(p,q)$ (say it is $T^{a_1a_2\dots a_p}_{\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ b_1b_2\dots b_q} $) along the direction $e_c$, the algorithm is to take the partial derivative of the tensor, and then add $\Gamma^{a_i}_{\ \ \ dc}$ for every upper index, and subtract $\Gamma^d_{\ \ b_i c}$ for every lower index ($i$ running for the proper distance).

Then for an arbitrary $(0,2)$ tensor, we have

$$\nabla_{i}T_{ab}=\partial_iT_{ab}-\Gamma^{d}_{\ \ \ ia}T_{db}-\Gamma^d_{\ \ \ ib}T_{ad}$$

Now, you already showed that

$$\nabla_jT_k=\partial_jT_k-\Gamma^{b}_{\ \ \ jk}T_b$$

Thus putting things together

\begin{align*}\nabla_{i}\nabla_jT_k&=\partial_i(\nabla_jT_k)-\Gamma^{d}_{\ \ \ ij}\nabla_dT_k-\Gamma^d_{\ \ \ ik}\nabla_jT_d \\&=\partial_i\partial_jT_k-\partial_i(\Gamma^{b}_{\ \ \ jk}T_b)-\Gamma^{d}_{\ \ \ ij}(\partial_dT_k-\Gamma^{b}_{\ \ \ dk}T_b)-\Gamma^{d}_{\ \ \ ik}(\partial_jT_d-\Gamma^{b}_{\ \ \ jd}T_b) \end{align*}

Now you can put $k=i$ and further simplify. It will be a mess of terms, but hopefully this helps!

thank you very much. If the implementation is right, computing $\frac{d\pi_{ij}}{dt}$ allows us to compute $\frac{dg_{ij}}{dt}$ at every location, which when compared will give the same result as the $g_{ij}$ value written at the $t+dt$ location, right? I am still a bit puzzled by what the program of ADM numerical relativity is, since no new insight is gained, and the full 4-dimensional time evolution must first be stitched/evolved manually into 4-dimensional grid data, what exactly do we gain by painstakingly calculating $\frac{d\pi_{ij}}{dt}$ and $\frac{dg_{ij}}{dt}$? — James, Feb 09 '23 at 15:04

James · Answer 2 · 2023-02-09T17:55:43.653

Expanding on what are already mentioned in the comments to full explicit form, let $v$ be the 3-dimensional vector field

$$v = \begin{pmatrix} v_0 \\ v_1 \\ v_2 \end{pmatrix}$$

The first order covariant derivative of $v$ is the 3-dimensional vector field:

$$ \nabla_i v = \begin{pmatrix} \frac{\partial v_0}{\partial i} - \Gamma^0_{i0}v_0 - \Gamma^0_{i1}v_1 - \Gamma^0_{i2}v_2 \\ \frac{\partial v_1}{\partial i} - \Gamma^1_{i0}v_0 - \Gamma^1_{i1}v_1 - \Gamma^1_{i2}v_2 \\ \frac{\partial v_2}{\partial i} - \Gamma^2_{i0}v_0 - \Gamma^2_{i1}v_1 - \Gamma^2_{i2}v_2\end{pmatrix}$$

Renaming this vector field as

$$ w = \begin{pmatrix} w_0 \\ w_1 \\ w_2 \end{pmatrix} = \nabla_i v$$

We can now repeat the same procedure on $w$ to get to the second order covariant derivative of $v$:

$$ \nabla_{ji} w = \nabla_j \nabla_i v = \begin{pmatrix} \frac{\partial w_0}{\partial i} - \Gamma^0_{i0}w_0 - \Gamma^0_{i1}w_1 - \Gamma^0_{i2}w_2 \\ \frac{\partial w_1}{\partial i} - \Gamma^1_{i0}w_0 - \Gamma^1_{i1}w_1 - \Gamma^1_{i2}w_2 \\ \frac{\partial w_2}{\partial i} - \Gamma^2_{i0}w_0 - \Gamma^2_{i1}w_1 - \Gamma^2_{i2}w_2\end{pmatrix}$$

There are 3 first order covariant derivative vector fields of $v$,

$$\nabla v = \begin{bmatrix}\nabla_0 v \\ \nabla_1 v \\ \nabla_2 v\end{bmatrix}$$

and there are 3x3 second order covariant derivative vector fields of $v$,

$$\nabla^2 v = \begin{bmatrix}\nabla_0\nabla_0 v & \nabla_0\nabla_1 v & \nabla_0\nabla_2 v \\ \nabla_1\nabla_0 v & \nabla_1\nabla_1 v & \nabla_1\nabla_2 v \\ \nabla_2\nabla_0 v & \nabla_2\nabla_1 v & \nabla_2\nabla_2 v\end{bmatrix}$$

score 0 · Answer 3 · answered Feb 09 '23 at 18:05

The covariant derivative is generalizable to tensors of any shape. For a vector [(1,0) tensor] $v$, its covariant derivative has the components $$(\nabla v)^i{}_j=\partial_jv^i+\Gamma^{i}_{jk}v^k$$ For covectors [(0,1) tensors] it is similar: $$(\nabla\omega)_{ij}=\partial_j\omega_i-\Gamma^k_{ij}\omega_k$$ For a tensor $T$ of shape $(r,s)$, you just repeat the above for as many indices as are necessary:

$$ ( \nabla T)^{i_{1} \dotsc i_{r}}{}_{j_{1} \dotsc j_{s} \ k} =\begin{matrix} \partial _{k} T^{i_{1} \dotsc i_{r}}{}_{j_{1} \dotsc j_{s}}\\ +\Gamma _{lk}^{i_{1}} T^{l\ i_{2} \dotsc i_{r}}{}_{j_{1} \dotsc j_{s}} +\cdots +\Gamma _{lk}^{i_{r}} T^{i_{1} \dotsc i_{r-1} \ l}{}_{j_{1} \dotsc j_{s}}\\ -\Gamma _{j_{1} k}^{l} T^{i_{1} \dotsc i_{r}}{}_{l\ j_{2} \dotsc j_{s}} -\cdots -\Gamma _{j_{s} k}^{l} T^{i_{1} \dotsc i_{r}}{}_{j_{1} \dotsc j_{s-1} \ l} \end{matrix}$$

Using $T=\nabla N$ will give you what you are looking for.

What is $\nabla_i \nabla _j N_i$ in differential geometry?

3 Answers3