I originally asked this on Stack Overflow, it was suggested that I ask here.
I need to find the maximum volume inscribed ellipsoid subject to linear inequality constraints and a constraining ellipsoid. I've been stuck on this for quite some time and have made very little progress.
I have it worked out for the linear constraints, but am having issues with the ellipsoidal constraint.
I'm trying to follow section 8.4.2 of Boyd & Vandenberghe —Maximum volume inscribed ellipsoid, subsection: Maximum volume ellipsoid in an intersection of ellipsoids.
Originally I had NxN PSD matric B and Ndim vector d being the optimization variables (shape and location of ellipse), but I needed to introduce another scalar variable $\lambda$ to follow the book. Additionally I added parameters P and b (where P would be A_1 in the excerpt, as there is only one ellipsoid constraint in my case, and b I think would be b_1 but could be c_1) being the constraining ellipsoid's shape and location. Lastly added a parameter c for the constraining ellipsoid.
I don't understand the purpose of λ and c; I assume they are scaling factors, but I was under the impression that matrices B and P determine the size of the ellipses. I have no idea what the value of c should be set to; my best guess it 1, but running that code says it's infeasible when it clearly is when I plot the ellipse (I get the values to plot like so:
B.value @ np.array([ np.cos(angles) , np.sin(angles) ]) + d.value @ np.ones( (1, noangles) )
which is another reason that λ and c are confusing me; where do I use them?).
I think there's probably an issue in the code for creating this constraint matrix
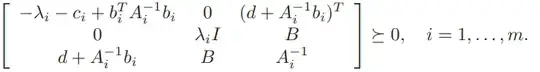 , but I can't find it. I couldn't use bmat because the shapes of the elements didn't allow for it. The shape of each element in my simple test case is:
, but I can't find it. I couldn't use bmat because the shapes of the elements didn't allow for it. The shape of each element in my simple test case is:
[[(1, 1), (1, 2), (1, 2)],
[(2, 1), (2, 2), (2, 2)],
[(2, 1), (2, 2), (2, 2)]]
so I composed them like this:
left = cp.vstack([np.zeros((n,1)),
d + P_inv@b])
lower_right = cp.bmat([[(λ*np.identity(n)), B ],
[B, P_inv ]])
bottom = cp.hstack([left,lower_right])
top = cp.hstack([-λ - c + cp.quad_form(b,P_inv), np.zeros((1,n)), (d + P_inv@b).T])
block_mat = cp.vstack([top,bottom])
ellipse_constraint = PSD(block_mat)
When c is set to 1, the problem is infeasible, 0 and lower works but the solution it returns is much smaller than (and seemingly rotated $90$ degrees from) the constraining ellipsoid when I plot them.
So, I want to know if $\lambda$ and $c$ are necessary, and if so, how to incorporate them into the plotting so I can verify the process is working and how do I determine what value to set c to, as well as if there is a glaring mistake in how I create the ellipsoidal constraint.
