2

Which regular n-gons can be tiled by (or tessellated into) a finite number of non-overlapping parallelograms?

I have enumerated a few cases below where I know the answer:

  • Case $n = 3$, there is evidently no solution for any triangle.

  • Case $n = 4$, the square is already a parallelogram so that's trivial.

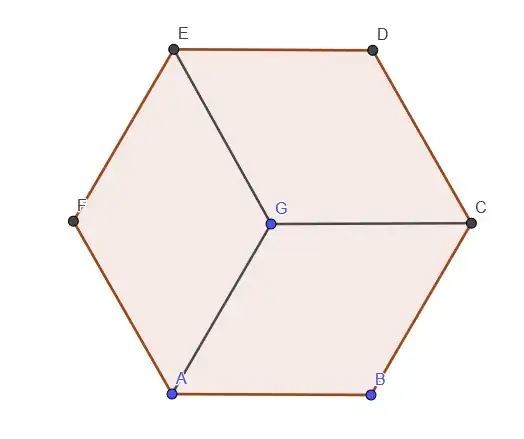
  • Case $n = 6$, the regular hexagon admits a nice tessellation as follows:

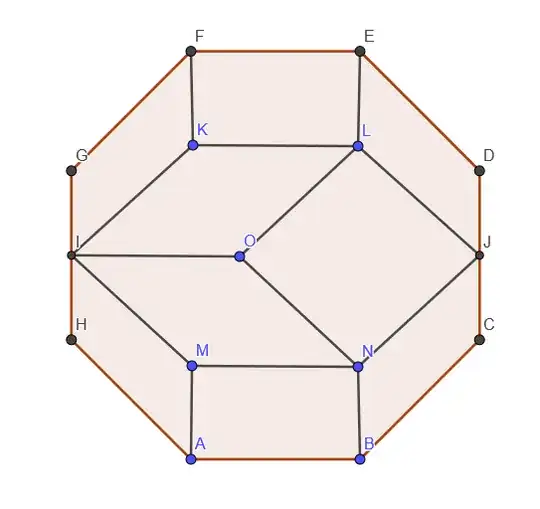
enter image description here

  • Case $n = 8$, I have found the following tessellation for a regular octagon, though perhaps there is a simpler one:

enter image description here

(please forgive the approximate geometric shapes, I am freehanding it to show the idea)

I am particularly interested in a solution for the regular pentagon and heptagon, though the fact they have no parallel "opposite" sides due to having an odd number of sides makes me feel like a tessellation shouldn't exist for these, but I have no proof of this.

Has this problem been studied or does anyone have any insights into how to approach it?

I have already seen this question which is more specific than mine as it requires rhombuses whereas I am satisfied with more general parallelograms.

Thomas
  • 962
  • 1
    The paper Tiling polygons with parallelograms seems relevant for your question. – VTand Feb 01 '23 at 11:47
  • 1
    @VTand Indeed, I think Theorem 1 in that paper pretty much settles it, implying a regular n-gon is tileable if and only if n is even... and even provides a construction which does the octagon in 6 tiles whereas mine above has 9. Great find ,I think this can be posted as an answer if you'd like? – Thomas Feb 01 '23 at 12:00

1 Answers1

3

In the paper Tiling polygons with parallelograms (https://doi.org/10.1007/BF02187834), Section 3 states the following:

The edges of the polygon can be partitioned into equivalence classes where two edges are in the same class if they are parallel. We call the equivalence classes slope classes.

Balance Condition. In every slope class, $S$, the vector sum of all the (oriented) edges in $S$ is zero.

Theorem 1. A convex polygon is tilable if and only if it respects the balance condition.

It follows that a regular $n$-gon is tilable if and only if $n$ is an even integer (and $n \geq 4$).

VTand
  • 2,789