Prove that $\angle AED = 2 \cdot \angle BEC$

Question

Let $ABCDE$ be a pentagon such that $AE = ED$, $BC = DC + AB$ and $\angle BAE + \angle CDE = 180°$. Prove that $\angle AED = 2 \cdot \angle BEC$.

So, by constructing it in Geogebra, I noticed that if I mark a point $F$ in $BC$ such that $CF = CD$ and $BF = AB$, then $EF = ED = AE$, and the triangles $\triangle CEF$ and $\triangle CDE$ are congruent. Same thing about $\triangle BEF$ and $\triangle BAE$. Then $\angle AEB = \angle BEF$ and $\angle CEF = \angle CED$ and then the problem is basically done. But how can I prove $EF = ED = AE$? I wasn't able to prove it, so I wasn't able to progress any further. I tried proving $\angle ECF = \angle ECD$, but still, I got stuck.

Answer 1

It is a great idea to split $BC$ so that we may use the condition $BC=DC+AB$ easily. However, the condition $\angle BAE + \angle CDE = 180^\circ$ remains isolated. A better idea could be trying to taking advantage of that condition together with the adjacent condition $AE=ED$ to bring up two congruent triangles.

---

Extend line segment $BA$ to $AF$ such that $AF=DC$.

This come along with two more perks:

• $\angle EAF=180^\circ-\angle BAE=\angle EDC$,
• $BC=DC+AB=AF+AB=BF$.

Since $\angle EAF=\angle EDC$, $AF=DC$ and $AE=DE$, we have $$\triangle EAF\cong\triangle EDC,$$ which implies $EF=EC$ and $\angle AEF=\angle CED$.

Since $BC=BF$, $EF=EC$ and $BE=BE$, we know $$\triangle BEC\cong\triangle BEF,$$ which implies $\angle BEC=\angle BEF$.

Hence, $$\angle AED-\angle BEC = \angle CED + \angle BEA= \angle AEF+\angle BEA= \angle BEF = \angle BEC$$

Answer 2

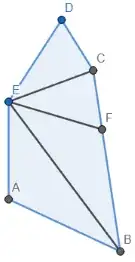
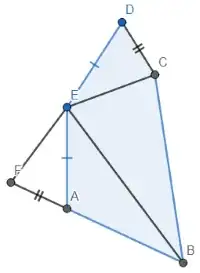
You've made a good start. We can prove $EF = ED = AE\;$ by using the law of cosines on several triangles and that $\cos(180^{\circ}-z)=-\cos(z)$. First, for somewhat simpler algebra, I've assigned several angle and length values as shown in the diagram below:

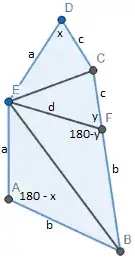
In particular, there's

$$AE=ED=a, \; AB=BF=b, CF=CD=c, EF=d, \measuredangle CDE = x, \measuredangle CFE = y \tag{1}\label{eq1A}$$

Thus, $\measuredangle BAE = 180^{\circ} - x$ and $\measuredangle BFE = 180^{\circ} - y$. Using the law of cosines for the common side of $EB$ in $\triangle EAB$ and $\triangle EFB$, we get

$$\begin{equation}\begin{aligned} EB^2 & = a^2 + b^2 + 2ab\cos(x) \\ & = b^2 + d^2 + 2bd\cos(y) \end{aligned}\end{equation}\tag{2}\label{eq2A}$$

The first line subtract the second line gives

$$a^2-d^2 +2b(a\cos(x) - d\cos(y)) = 0 \tag{3}\label{eq3A}$$

Next, using the law of cosines for the common side of $EC$ in $\triangle EDC$ and $\triangle EFC$ gives

$$\begin{equation}\begin{aligned} EC^2 & = a^2 + c^2 - 2ac\cos(x) \\ & = c^2 + d^2 - 2cd\cos(y) \end{aligned}\end{equation}\tag{4}\label{eq4A}$$

As before, the first line subtract the second line gives

$$a^2 - d^2 - 2c(a\cos(x) - d\cos(y)) = 0 \tag{5}\label{eq5A}$$

Next, \eqref{eq3A} subtract \eqref{eq5A} gives, since $b \gt 0$ and $c \gt 0$, that

$$2(b+c)(a\cos(x)-d\cos(y)) = 0 \; \; \to \; \; a\cos(x)-d\cos(y) = 0 \tag{6}\label{eq6A}$$

Substituting this in either \eqref{eq3A} or \eqref{eq5A}, and using \eqref{eq1A}, gives

$$a^2 - d^2 = 0 \; \; \to \; \; a = d \; \; \to \; \; EF = ED = AE \tag{7}\label{eq7A}$$

Answer 3

I’ll try to motivate every step.

To make use of the condition $BC=DC+AB$ we’ll split the segment $BC$ into two parts by defining a point $X\in BC$ such that $CD=CX$ and $BA=BX$. Now what does the condition $\angle BAE+\angle CDE=180$ remind you of? well for me it’s cyclic quadrilaterals. So we’ll try to construct one by defining $Y=AB\cap DC$. Now we have $AYDE$ is cyclic. If you look closely now you might notice that $EC\perp DX$ and $EB\perp AX$ and in fact it one of these two is true then $ED=EX=EA$ and $\angle DEA= \angle DEX+ \angle XEA=2(\angle CEX+BEX)=2 \angle CEB$ and we’d be done.

To prove this note that up until now we didn’t use the conditions $ED=EA$ and $CD=CX$ so if we let $M$ be the midpoint of $AD$ and $F$ the midpoint of $DX$ then $\angle EMD= 90^{\circ}$ and now I hope you can see the cyclic quadrilateral $EMFD$. Proving this will finish off the problem.

Luckily this is just angle chasing $$\angle DEM=\frac{1}{2}\left(\angle DEA\right)= \frac{1}{2}\left( 180^{\circ}-\angle DYA\right) =180^{\circ}-\angle DXA=180^{\circ}-\angle DFM$$ (I didn't write the full angle chase). Feel free to ask if some step wasn't motivated for you. By the way what’s the source of the problem?