3

Let $D$ be a convex subset of $\Bbb R^n$. Every monotone increasing transformation of a convex function is quasi-convex. Does the converse hold?

Question. Given a continuous quasi-convex function $f:D \to \Bbb R$, does there exist a continuous, strictly increasing function $\phi:\Bbb R \to \Bbb R$ such that the composition $\phi \circ f$ is convex?

Note. If $\phi$ was not required to be strictly increasing, then we could choose $\phi$ being a constant.

Two equivalent definitions of quasi-convexity:

Definition 1. A function $f:D \to \Bbb R$ is quasi-convex iff its epigraph is convex.

Definition 2. A function $f:D \to \Bbb R$ is quasi-convex iff $$ f\big((1-\lambda)a+\lambda b\big) \leq \max\big\{ f(a), f(b) \big\} \qquad \forall a,b\in D, \lambda \in [0,1]. $$

Pavel Kocourek
  • 1,648

1 Answers1

1

I thought that the answer was yes and I only found out how I was mistaken when I was trying to prove its extension into "third-order quasi-convexity". That is why I decided to share this observation just in case I was not the only one confused about this.

There are two cases for any quasi-convex function $f:\Bbb R \to \Bbb R$:

  • $f$ is monotone: then we can put $\phi=f^{-1}$, so that $\phi\circ f(x)=x$ is a convex function ($\phi \circ f$ represents the function $x\mapsto \phi(f(x))$);
  • $f$ is decreasing and then increasing: (both in weak sense) Then we can "correct" the left (decreasing) and right part of $f$ individually in the sense that applying $\phi$ to $f$ makes $\phi\circ f$ convex, but it might be impossible to correct both left and right parts of $f$ simultaneously:

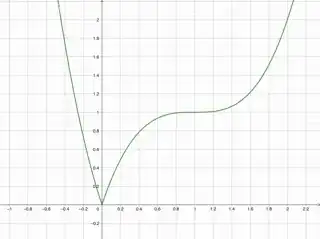
Contraexample. The function $f(x)=|1+(x-1)^3|$ is quasi-convex because it is decreasing on $(-\infty,0]$ and increasing on $[0,\infty)$, but any transformation $\phi$ that would make $\phi\circ f$ convex on $[0,\infty)$ would fail making $\phi \circ f$ convex on $(-\infty,0]$.
Graph of the function

Proof. The conflict relies in the fact that $f'(1)=0$, by $f'(x_0)\neq 0$ at the point $x_0<0$ such that $f(x_0)=2=f(1)$. For a contradiction suppose that was a strictly increasing function $\phi$ such that $g\equiv \phi\circ f$ is convex.

WLOG, assume that $\phi(0)=0$ and $\phi(1)=1$. Then $g(0)=0$ and $g(1)=(x_0) = 1$.

For any $\varepsilon>0$, we have $$ g(1)\leq \frac{\varepsilon}{1+\varepsilon} g(0) + \frac{1}{1+\varepsilon} g(1+\varepsilon), $$ $$ 1\leq\frac{1}{1+\varepsilon} g(1+\varepsilon), $$ $$ \varepsilon\leq g(1+\varepsilon)-g(1), $$ $$ 1\leq \frac{g(1+\varepsilon)-g(1)}{\varepsilon}. $$ Substituting $g(1+\varepsilon) = \phi(1+\varepsilon^3)$ in the above inequality $$ 1\leq \frac{\phi(1+\varepsilon^3)-\phi(1)}{\varepsilon}, $$ $$ \varepsilon^{-2} \leq \frac{\phi(1+\varepsilon^3)-\phi(1)}{\varepsilon^3}, $$ which letting $\varepsilon \to 0$ gives us that the right derivative $\partial_+\phi(1) = \infty$. Consequently, $$ \partial_- g(x_0) = \partial_ \phi(f(x_0)) = \partial_+\phi(1) \cdot f'(x_0) = -\infty. $$ However, it is known that the left/right derivative of a convex function can be infinite only at the boundary of its domain. Contradiction. $\tag*{$\Box$}$

Note. The function $f$ from the contra-example is in fact strictly quasi-convex.

Pavel Kocourek
  • 1,648