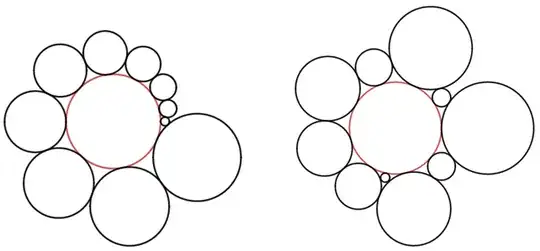
Non-overlapping circles of radius $1, 2, 3, ..., n$ are all externally tangent to a middle circle.
How should we arrange the surrounding circles, in order to minimize the middle circle's radius $R$?
Take $n=10$ for example.
On the left, going anticlockwise the radii are $1, 2, 3, 4, 5, 6, 7, 8, 9, 10$, and $R\approx 10.77$.
On the right, going anticlockwise the radii are $10, 2, 9, 4, 7, 6, 5, 1, 8, 3$ and $R\approx 9.98$.
How should the circles be arranged to minimize $R$?
Here is a desmos graph where you can try different arrangements for the case $n=10$.
My attempt
For general $n$, call the radii of the surrounding circles going anti-clockwise, $r_1, r_2, r_3, ..., r_n$.
Draw line segments from the centre of the middle circle to the centre of each surrounding circle. So we have $n$ angles at the centre of the middle circle. Each of these angles can be expressed in terms of $R, r_k, r_{k+1}$, using the law of cosines. The sum of the $n$ angles is $2π$. So we have:
$$\sum\limits_{k=1}^n \arccos{\left(\frac{(R+r_k)^2+(R+r_{k+1})^2-(r_k+r_{k+1})^2}{2(R+r_k)(R+r_{k+1})}\right)}=2\pi \text{ (where }r_{n+1}=r_1)$$
This simplifies to:
$$\sum\limits_{k=1}^n \arccos{\left(1-\frac{2r_k r_{k+1}}{(R+r_k)(R+r_{k+1})}\right)}=2\pi$$
We want to assign each $r$ a unique value among $1, 2, 3, ..., n$ so that $R$ is minimized. But how? Is there a general pattern?
Conjectured answer
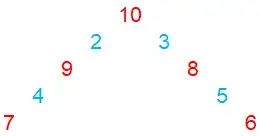
I think the following general procedure will make the middle circle as small as possible. Take $n=10$ for example. We ignore the $1$ at first; it will be placed last. First put down the numbers $10, 9, 8, 7, 6$ in pyramid-fashion, from top to down and from left to right, like the red numbers below. Then put down the numbers $2, 3, 4, 5$ in pyramid-fashion also, but between the previous rows, like the blue numbers below.
This gives the order of radii going around the circle: $7, 4, 9, 2, 10, 3, 8, 5, 6$. Then put the circle with radius $1$ anywhere you like, as long as it fits without disturbing other circles.
For larger values of $n$, there may be multiple small circles that can fit between other circles without disturbing them. Put those last.
Intuitively, this procedure minimizes the tendency of the large surrounding circles to take up space around the middle circle. You can see this in the diagrams above with $n=10$, looking specifically at the two largest surrounding circles in each case.
Anyway, it's just a conjecture for now. Notice that this conjecture implies that, for $n=10$, the arrangement I showed above on the right, yields the minimum radius of the middle circle. I don't think the middle circle can be any smaller.