According to this topic, we understand well the relation between the ergodicity for dynamical system and the mean ergodicity of a stochastic process. More exactly, we have the Ergodic Theorem (See page 413 of A. N. Shiryaev)
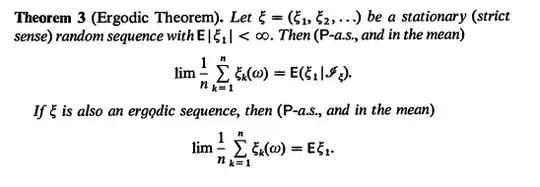
The following definition is about a random process $(Y_t)_{t \in \mathbb Z}$
where $\gamma_j := E(Y_t - \mu)(Y_{t-j} - \mu)$, with $\mu=E Y_t$.
But now where does it come in or how do these ergodic concepts of dynamical systems relate to the concept of ergodicity for the second moments?
