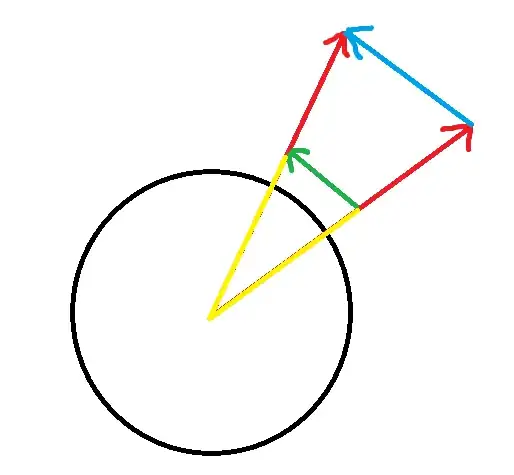
The Christoffel symbols for polar coordinates r base vector are:
$$\Gamma_{r\theta}^r=0$$
$$\Gamma_{r\theta}^\theta=\frac{1}{r}$$
I understand intuitively why the first one is true: the rate of change of r basis vector in radial direction is zero.
I have difficulty understanding why the second one is true. It says that at large r, the rate of change of r basis vector in azimuthal direction is close to zero. My intuition tells me that the rate of change in azimuthal direction should be bigger (ie. proportional to r).
To illustrate my confusion, in the diagram above the rate of change of the smaller r basis vector (yellow) is represented by the green arrow. The rate of change of the bigger r basis vector (red) is represented by the blue arrow. So $\Gamma_{r\theta}^\theta$ should be proportional to r.
What am I missing?