3

This question has the answer here by Hagen von Eitzen. I consider the proof as unwantedly lengthy. I am looking to simplify the proof.

My proof:

Consider a convex shape $S$ of positive area $A$ inside the unit square. Let $a\le 1$ be the supremum of all subsets of the unit square that can be obtained as disjoint union of finitely many scaled and translated copies of $S$.

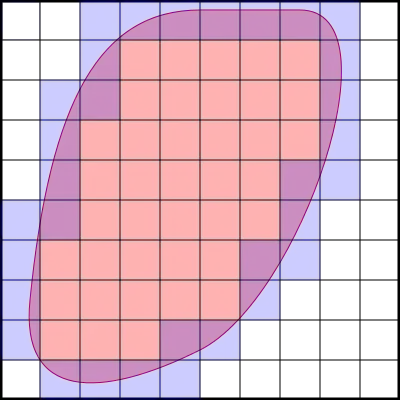
Partition the square into $n\times n$ smaller squares (see picture). There are three types of such small squares: $e$ exterior squares (white in the picture), $i$ interior squares (light red in the image) and $b$ boudary squares (blue/purple). Of course $e+b+i=n^2$

enter image description here

$$\dfrac{i}{n^2} < A$$

$$\implies\dfrac{i}{n^2} + \dfrac{b}{n^2} < A + \dfrac{b}{n^2} \tag1$$

Picking a finite packing that covers $\ge a-\epsilon$, for some $\epsilon$, we can put a scaled-down copy of this packing into each of the $e$ "white" squares and, together with the original shape $S$, obtain a finite packing of the unit square that covers $e \dfrac{a- \epsilon}{n^2} + A$

\begin{align} \text{Area of finite disc packing} &= e \dfrac{a- \epsilon}{n^2} + A \tag2 \end{align}

\begin{align} a>\text{Area of finite disc packing} &= e \dfrac{a- \epsilon}{n^2} + A \tag {by 2}\\ &= \dfrac{e}{n^2} (a- \epsilon) + A \\ &= \left[ 1- \left( \dfrac{i}{n^2} + \dfrac{b}{n^2} \right) \right] (a- \epsilon) + A\\ &\geq \left[ 1- \left( A + \dfrac{b}{n^2} \right) \right] (a- \epsilon) + A \tag {by 1}\\ &=\left[ 1 - A - \dfrac{b}{n^2} \right] (a- \epsilon) + A \end{align}

$$\implies \left[ 1 - A - \dfrac{b}{n^2} \right] (a- \epsilon) + A<a$$

As $n\to\infty$ and $\epsilon\to 0$ the LHS converges to $a+(1-a)A$. According to a limit theorem, this limit must be $\le a$. Thus we conclude $a=1$.

My question:

Is my proof correct and sufficient?

lorilori
  • 556
  • 3
    That user is still active on the site...why not post a comment on their answer to get their direct attention? – lulu Dec 23 '22 at 01:20
  • I am going to do it... But am I correct? – lorilori Dec 23 '22 at 01:21
  • 2
    I have not studied either the original post nor your proposed simplification of it. This post is not self-contained, which is why I am suggesting you try to go back to the source. – lulu Dec 23 '22 at 01:22
  • 1
    let me make this question self contained... – lorilori Dec 23 '22 at 01:41
  • a) Did you use at any point that the shape $S$ is convex? - b) Is the claim even true for non-convex $S$? (Indeed one only needs something much weaker than convexity, namely it suffices that the Lebesgue measure of the boundary is zero; my counting argument for $b$ was a poor-man‘s-proof of that measure property) – Hagen von Eitzen Dec 24 '22 at 15:02

1 Answers1

2

No, your proof doesn't quite work.

The difference between your attempt vs Hagen's original proof is that they used the extra step $b \le 8(n-1)$ so their final expression before the limit step was $$a > \left(1-A-\frac{8}{n} \right) (a-\epsilon) + A.$$

At that point, it's valid to take the limits as $n \to \infty$ and $\epsilon \to 0$ and we're done.

In your proof, you've attempted to simplify the argument by skipping the $b \le 8(n-1)$ step. Your final expression before taking limits is $$\left[ 1 - A - \dfrac{b}{n^2} \right] (a- \epsilon) + A<a.$$

This time it isn't valid to take the limits you need, because your expression includes $b$ which depends on both $\epsilon$ and $n$ in some confusing way. What if $b$ turned out to grow extremely fast as you choose $n$ large and $\epsilon$ small?

This issue is why the other author went out of their way to bound $b$ so that they could create a final expression that just depends on $a, A, n$, and $\epsilon$ before taking limits. (It's fine to still have $a$ and $A$ in the expression because those don't depend on $n$ or $\epsilon$.)

David Clyde
  • 5,399
  • Thank you so much... Can you help me extend this theorem for sphere in three dimensions? This is the problem whose solution I am seeking for the last 3 days... Only help me to construct the analogous inequality as $b \le 8(n-1)$ for a sphere in 3D. – lorilori Dec 23 '22 at 10:48
  • 1
    The 3D version should show $b \le c (n-1)^2$. Then you can use the same argument from there. To prove that inequality you could repeat basically Hagen's argument, except instead of the $n-1$ vertical lines, there are now $(n-1)^2$ vertical lines instead (and same for lines in each of the other two axis directions). You should look at Hagen's proof and think about this and if you still have trouble then it's probably better to post a separate question instead of adding a bunch of detailed proofs in the comments here. – David Clyde Dec 23 '22 at 11:09
  • 1
    Can you answer this question, if possible? – lorilori Dec 23 '22 at 11:59